uabooks.top

A váltakozó áram erősségének pillanatnyi értéke állandóan változik - periodikusan hol nullává alakul, hol maximális értéket ér el. De akkor miért úgy mondjuk, hogy „az áramerősség a lámpa izzószálán 0,27 A", vagy „a mosógép fűtőszálán átfolyó feszültség 220 V"? Tisztázzuk, hogy a váltakozó áram milyen erősségéről és feszültségéről is beszélünk.

Milyen ellenállást neveznek aktívnak?

Az egyenáramot tanulmányozva megtudtátok, hogy minden vezető (kivéve a szupravezetőket) rendelkezik ellenállással. A vezetők a váltakozó árammal szemben is tanúsítanak ellenállást, viszont a váltakozó áramú körökben, az egyenáramtól eltérően, az ellenállásnak különböző fajtái léteznek, amelyeket két csoportra oszthatunk: aktív és reaktív ellenállásokra.

Az elektromos áramkör eleme R aktív ellenállással rendelkezik, ha a rajta átfolyó áram elektromos energiájának egy része melegítésre fordítódik:

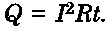
A változó áramú áramkör bármely eleme (összekötő vezetékek, fűtőszálak, a motorok, generátorok, transzformátorok tekercsei), mint ahogyan az egyenáram esetében is, aktív ellenállással rendelkezik (mi egyszerűen csak ellenállásnak nevezzük).

Vizsgáljunk meg egy elektromos áramkört, amely összekötő huzalokból, kis induktivitású, de jelentős R aktív ellenállású terhelésből és váltakozó áramú áramforrásból áll (20.1. a ábra). A kör kimenetelén a feszültség harmonikus törvény szerint váltakozik:

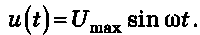
Ohm törvénye alapján az áramerősség a körben szintén harmonikusan váltakozik:

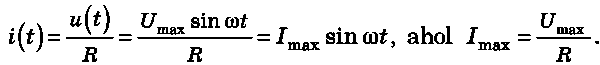
Az elektromos áramkör azon elemeiben, amelyek kizárólag aktív ellenállással rendelkeznek, az áramerősség és feszültség rezgési fázisa azonos (20.1. b ábra).

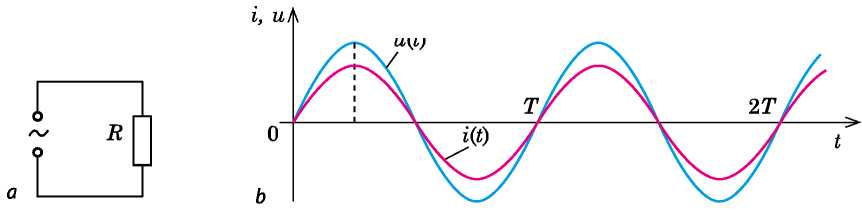
20.1. ábra. Aktív ellenállás váltakozó áramú körben: a - a kör kapcsolási rajza; b - az i(t) és u(t) függvények grafikonjai. Az áramerősség és feszültség egy időben éri el maximális értékét és egy időben lesz nulla

Hogyan határozható meg az áramerősség és feszültség effektív értéke?

A váltakozó áram hatásának meghatározása a pillanatnyi áramerősség alapján nem célszerű, hiszen az értéke állandóan változik. Átlagértékeket sem alkalmazhatnak, mivel az áramerősség értéke egy periódus alatt nulla (20.1. b ábra). A váltakozó áram hatását az áramerősség effektív értéke alapján értékelik.

Tételezzük fel, hogy van két darab, egyenként R ellenállással rendelkező izzólámpánk. Az egyiket egyenáram forrásához kapcsoltuk, a másikat pedig váltakozó áraméhoz (20.2. ábra). A reosztát csúszkáját elmozdítva mindkét izzó fényességét azonos szintre hozzuk. Ez azt jelenti, hogy a váltakozó áram teljesítményének átlagértéke egyenlő az egyenáram teljesítményével:

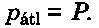
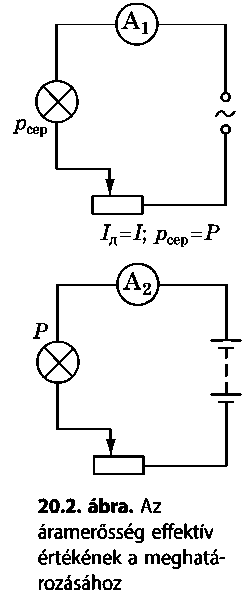
Az áramerősség I_e effektív értéke azzal az egyenáramú / áramerősséggel egyenlő, amikor a legaktívabb ellenállás mellett P teljesítmény szabadul fel, ami megegyezik a váltakozó áram jD_átl átlagos teljesítményével:

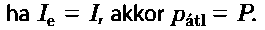
Az R aktív ellenállással rendelkező izzólámpa által felhasznált egyenáram teljesítménye: P = PR.

Meghatározzuk a váltakozó áram teljesítményének átlagértékét. Végtelenül kis időintervallumban az áramerősséget változatlannak tekintjük, ezért a pillanatnyi teljesítmény a p = i²R képlet segítségével határozható meg, ahol

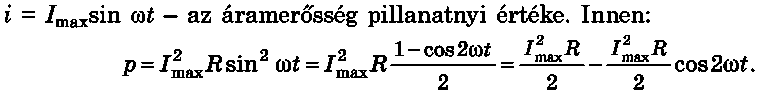
A pillanatnyi teljesítmény-idő grafikonból (20.3. ábra) látható, hogy a teljesítmény periódusbeli átlagértéke:

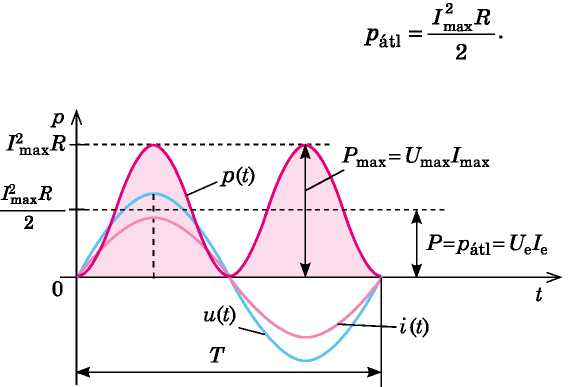
20.3. ábra Aktív ellenállás váltakozó áramú áramkörben: a p(t) grafikon - a teljesítmény időfüggésének grafikonja

Jegyezzétek meg!

Ha a váltakozó áramú áramkör csak aktív ellenállást tartalmaz, vagy ha a kör reaktív ellenállása nulla, akkor az áram által felszabadított Q hőmennyiséget, a váltakozó áram A munkáját és P teljesítményét a megfelelő' egyenáramú képletekkel határozzák meg:

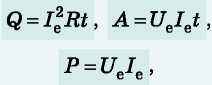
ahol U_e, I_e - a feszültség és árameró'sség effektív értékei.

Ha az áramkör reaktív ellenállása nem nulla, akkor az árameró'sség és feszültség fázisai eltérnek (meghatározott φ fáziseltolódásuk van). Ebben az esetben a váltakozó áram munkáját és teljesítményét a következő' képletekkel határozzák meg:

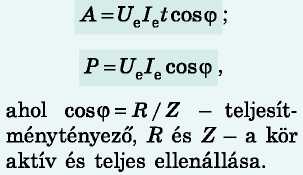
Mivel

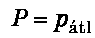
a következó't kapjuk:

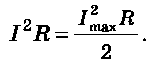
Innen a váltakozó áram erejének effektív értéke egyenlő:

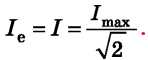
Hasonlóképpen a váltakozó feszültség effektív értéke egyenlő:

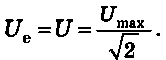
A gyakorlatban a váltakozó áram paramétereinek jellemzésére az árameró'sség és a feszültség effektív értékét alkalmazzák. Például amikor azt mondják, hogy a váltakozó áramú hálózatban a feszültség 220 V, az árameró'sség a körben 25 A, akkor ez azt jelenti, a feszültség effektív értéke a hálózatban 220 V, az árameró'sség effektív értéke pedig 25 A. A váltakozó áramú amperméterek és feszültségmérők az árameró'sség és a feszültség effektív értékeit mérik.

Reaktív ellenállás váltakozó áramú körben

A váltakozó áramú körbe kapcsolt kondenzátor és indukciós tekercs az áram számára pótlólagos ellenállást jelent. Ezt az ellenállást reaktívnak nevezzük, mivel a leküzdésükre nem használódik az áramforrás energiája. Egy negyed periódus alatt a kondenzátor és a tekercs energiát vesz el az áramforrástól, majd a következő negyed periódus alatt visszaadja azt.

A reaktív ellenállás fajtái

A vezető X_L induktív ellenállása önindukciós EME által a vezetőben kiváltott ellenállást jellemző fizikai mennyiség:

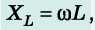
ahol ω - a váltakozó áram ciklikus frekvenciája; L — a vezető induktivitása.

Az X_c kapacitív ellenállás a kondenzátornak a váltakozó árammal szembeni ellenállását jellemző fizikai mennyiség:

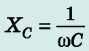
ahol ω — a váltakozó áram ciklikus frekvenciája; C - a kondenzátor kapacitása.

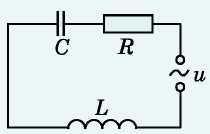
Az aktív, induktív és kapacitív ellenállással rendelkező áramkör teljes ellenállása a következő képlettel határozható meg:

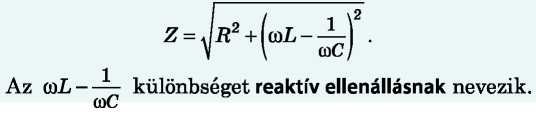
Összegezés

Az elektromos áramkör eleme R aktív ellenállással rendelkezik, ha a rajta átfolyó áram elektromos energiájának egy része

belső energiává

alakul át.

• Ha az elektromos áramkörben csak R aktív ellenállás van és a feszültség az áramforrás pólusain harmonikusan az

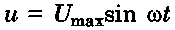
törvény szerint változik, akkor az áramerősség a körben szintén harmonikusan fog változni a

következő törvény alapján:

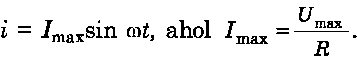
Eközben az áram

erősség és feszültség rezgéseinek fázisa megegyezik.

A váltakozó áram hatását az áramerősség és feszültség effektív értékei

határozzák meg:

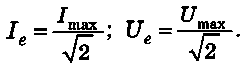
Ellenőrző kérdések

1. Az ellenállások mely típusaival találkozhatunk váltakozó áramú körben? Definiáljátok őket! 2. Milyen kapcsolat van az áramerősség és feszültség között az aktív ellenállású körben? 3. Mit nevezünk az áramerősség effektív értékének?

4. Hogyan számítható ki az áramerősség és feszültség effektív értéke? 5. Ismertessétek az induktív ellenállás képletét! Milyen tényezőktől függ? 6. Mit nevezünk kapacitív ellenállásnak? Milyen tényezőktől függ? 7. Mivel egyenlő az áramkör teljes ellenállása?

20. gyakorlat

1. A világításra szolgáló váltakozó áramú körökben 220 V feszültségű áramot használnak.

a) Mennyit mutat a körhöz kapcsolt voltméter?

b) Mennyi a maximális értéke a feszültségnek ezekben a körökben?

2. A 20 mH induktivitású tekercset 50 Hz frekvenciájú váltakozó áramú áramkörbe kapcsolták. Határozzátok meg a tekercs induktív ellenállását!

Az áramkör 900 Ω aktív ellenállású szakaszán az áramerősség az ί = Ο,δβΐηΙΟΟπί (A) függvény szerint váltakozik. Határozzátok meg: a) az áramerősség és a feszültség effektív értékeit; b) a szakaszon létrejövő teljesítményt; c) azt a feszültséget, amelyre a vezető szigetelését kell tervezni! írjátok fel az u(t) függvény egyenletét!

Az 1 pF kapacitású kondenzátort 50 Hz frekvenciájú váltakozó áramú áramkörbe kapcsolták. Határozzátok meg az áramerősséget az áramkör kondenzátort tartalmazó szakaszán, ha az adott szakasz összekötő vezetékeinek ellenállása 5 Ω, feszültsége — 12 V!

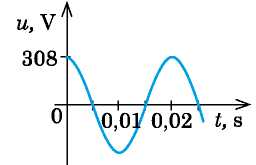
5. A rajzon a hálózati feszültség és idő közötti összefüggés grafikonja látható. Mennyi idő alatt forr fel a teafőzőben lévő 1,5 1 víz, ha a fűtőszál ellenállása 20 Ω, a teafőző hatásfoka 72%, a víz kezdeti hőmérséklete pedig 20 °С, a víz fajlagos hőkapacitása 4200 J/kg · °С?

6. Mint ismeretes, a kondenzátor két, egymástól szigetelőréteggel elválasztott vezetőből áll. Ezért az egyenáramú áramkörbe iktatott kondenzátor megszakítja az áramkört. Tudjátok meg, hogy akkor miért is vizsgálunk váltakozó áramú köröket kondenzátorral!

 

 

Fizika tankönyv 11. osztályosok szerzők Dovgy, Baryakhtar, Loktev