Момент імпульсу. Підставимо в основне рівняння динаміки обертального руху матеріальної точки M = Je вираз для кутового прискорення

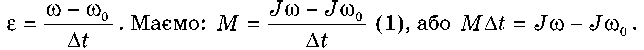
Ураховуючи, що для матеріальної точки момент інерції J = mr² ,

а кутова швидкість

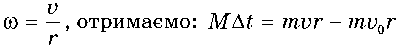
Величину mvr

називають моментом імпульсу матеріальної точки.

Момент імпульсу, L — це характеристика обертального руху матеріальної точки (чи системи матеріальних точок), що визначається відстанню точки від осі обертання, величиною та напрямком імпульсу відносно осі обертання: L = Jo = mvr.

Момент імпульсу є векторною величиною. Напрямок вектора моменту імпульсу збігається з напрямком вектора кутової швидкості.

Таким чином, формулу (1) можна записати як

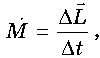
тобто момент

сили дорівнює зміні моменту імпульсу тіла за одиницю часу.

Закон збереження моменту імпульсу. Зміна моменту імпульсу тіла відбувається лише в результаті дії зовнішніх сил і залежить від моменту зовнішніх сил (обертального моменту). Якщо на тіло не діють зовнішні сили або їх рівнодійна не створює моменту відносно осі обертання M = 0, то зміна моменту імпульсу також дорівнює нулю: ΔJω = MΔt = 0. Якщо зміна величини ΔJω дорівнює нулю, сама величина залишається незмінною: Jo = const. Отже, ми познайомилися ще з одним законом збереження — законом збереження моменту імпульсу:

якщо на систему не діють моменти зовнішніх сил (замкнена система), то повний момент імпульсу системи тіл залишається постійним за величиною та напрямком:

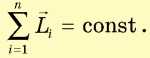
Збільшення моменту імпульсу одного з тіл має бути скомпенсованим відповідним зменшенням моменту імпульсу інших тіл системи.

Якщо розглядати окремо взяте тіло, яке не зазнає дії зовнішніх сил і не є твердим, тобто може змінювати свій момент інерції, то для такого тіла також виконується умова Jo = const. При цьому зміна моменту інерції (наприклад, збільшення) супроводжується відповідною зміною кутової швидкості (зменшенням). Продемонструємо це на прикладі.

Дівчинка стоїть на круглій платформі, яка може обертатися навколо нерухомої осі майже без тертя (мал. 107). Змінюючи положення рук (краще з гантелями), вона змінюватиме свій момент інерції, у результаті чого зміниться кутова швидкість обертання (мал. 107, б).

Цю властивість на практиці використовують балерини, акробати, танцівники, фігуристи під час виконання стрибків, переворотів тощо.

Кінетична енергія тіла, що обертається. Лінійна швидкість v матеріальної точки масою m, що обертається навколо осі О, може бути виражена через кутову швидкість ω й радіус обертання

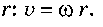
Вираз для кінетичної енергії в цьому разі набуває вигляду

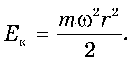
Добуток mr² є моментом інерції цієї точки відносно осі О, J = mr², отже,

для обертального руху

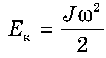
Цей вираз можна застосовувати для

всього тіла в цілому.

Отже, для загального випадку руху твердого тіла, що одночасно рухається поступально й обертається, наприклад котиться, повна кінетична енергія складається з кінетичної енергії поступального руху центра мас та енергії обертального руху відносно осі, що проходить через центр мас:

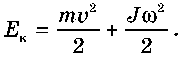
Зіставлення характеристик і рівнянь механіки поступального й обертального рухів (табл. 3).

Таблиця 3

ЗНАЮ, вмію, розумію

1. Що називають моментом імпульсу?

2. Сформулюйте закон збереження моменту імпульсу.

3. За якої умови зміна моменту інерції зумовлює зміну кутової швидкості? Як практично використовується прийом зміни моменту інерції?

4. Виведіть формулу кінетичної енергії тіла, що обертається.

5. Якою є кінетична енергія тіла, що котиться?

Приклади розв'язування задач

Задача 1. Горизонтальна платформа масою M і радіусом R обертається з кутовою швидкістю ω. На краю платформи стоїть людина масою m. З якою кутовою швидкістю ω₁ обертатиметься платформа, якщо людина перейде з краю платформи до її центра? Людину можна вважати матеріальною точкою, платформу — однорідним диском.

Задача 2. Горизонтальна платформа масою 80 кг і радіусом 1 м обертається навколо вертикальної осі, що проходить через її центр. У центрі платформи стоїть людина і тримає в розставлених руках гантелі. Плат-

форма обертається з кутовою швидкістю

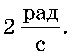
З якою кутовою швидкіс

тю почне обертатися платформа, якщо людина опустить руки і зменшить при цьому свій момент інерції від 3 до 1 кг · м²? Платформу вважайте круглим однорідним диском.

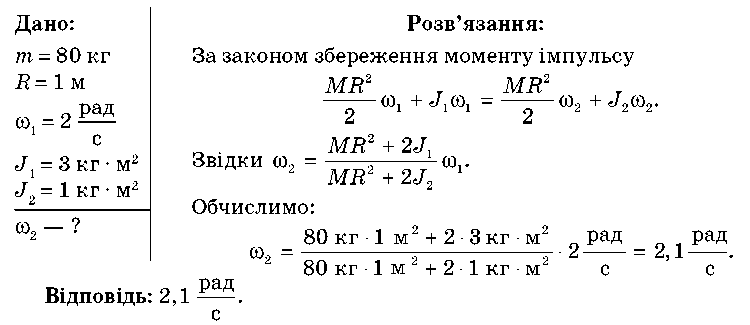
Задача 3. Маховик масою m та радіусом R обертається навколо осі, що проходить через його центр. Кутова швидкість обертання маховика — ω. Щоб зупинити маховик, до його обода притискають гальмівну колодку, яка діє на нього із силою F . Скільки обертів зробить маховик до повної зупинки? Вважайте, що маса маховика розподілена по ободу.

Розв’язання:

Розв’язуючи задачу, вважатимемо обертання маховика подібним до обертання тонкого однорідного обруча радіусом R і масою m, що обертається з кутовою швидкістю ω.

Кінетична енергія такого обруча:

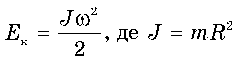
Маховик зупиниться за умови, що вся його кінетична енергія витратиться на роботу з подолання сили тертя F , що виникає між гальмівною колодкою та ободом, Е_к = F_Teps , де s — гальмівний шлях, що дорівнює

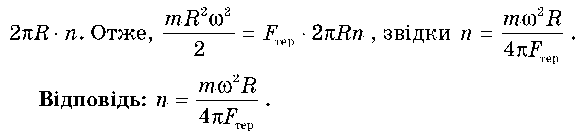
Задача 4. На барабан масою m = 9 кг намотано шнур, до кінця якого прив’язано вантаж масою m₀ = 2 кг. Визначте прискорення вантажу. Барабан вважайте однорідним циліндром. Тертям знехтуйте.

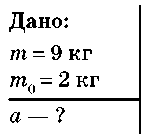
Розв’язання:

Під час опускання вантажу його потенціальна енергія зменшується й переходить у кінетичну енергію поступального руху вантажу та кінетичну енергію обертання барабана:

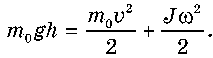
Оскільки для циліндра момент інерції

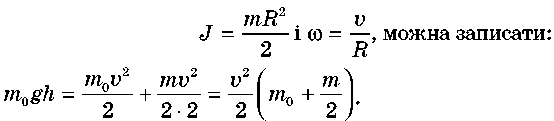
Рух рівноприскорений без початкової швидкості, отже,

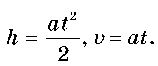
Підставляючи, отримуємо:

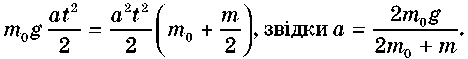
ВПРАВА 17

1. Спортсмен стоїть у центрі платформи, що обертається зі швидкістю

Спо

чатку спортсмен тримав гантелі на витягнутих руках на відстані 60 см від осі обертання. Як зміниться швидкість обертання платформи, якщо спортсмен зігне руки й гантелі опиняться на відстані 10 см від осі обертання?

2. Людина, що стоїть у центрі платформи, тримає в руках стержень завдовжки 2,4 м і масою 8 кг у вертикальному положенні (уздовж осі обертання платформи). Платформа з людиною обертається із частотою 1 с^-1. З якою частотою буде обертатися платформа, якщо людина поверне стержень у горизонтальне положення? Сумарний момент інерції людини і платформи — 6 кг · м^{1 2 3 4 5}.

3. На краю горизонтальної платформи, що має форму диска радіусом R = 2 м, стоїть людина масою m₁ = 80 кг. Маса платформи m₂ = 240 кг. Платформа може обертатися навколо вертикальної осі, що проходить через її центр. З якою кутовою швидкістю буде обертатися платформа, якщо людина буде йти вздовж її краю зі

швидкістю

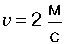
відносно платформи?

4. Платформа у формі диска може обертатися навколо вертикальної осі. На краю платформи стоїть людина масою m₁ = 60 кг. На який кут повернеться платформа, якщо людина піде краєм платформи і, обійшовши її по колу, повернеться в початкове положення? Маса платформи m₂ = 240 кг. Момент інерції людини розраховуйте як для матеріальної точки.

5. Доведіть, що людина, яка стоїть на ідеально гладкій горизонтальній поверхні, зможе провернутись навколо вертикальної осі, якщо почне обертати руку над головою.

6. Диск масою 2 кг котиться без тертя по горизонтальній поверхні зі швидкістю

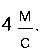
Визначте кінетичну енергію диска.

7. Мідна куля радіусом 10 см обертається із частотою

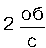
навколо осі, що прохо

дить через її центр. Яку роботу потрібно виконати, щоб збільшити кутову швидкість обертання кулі вдвічі?

8. Космічний корабель обертався в міжзоряному просторі з кутовою швидкістю ω. По команді із Землі на ньому відкрились антени, внаслідок чого момент інерції корабля збільшився у 2 рази. Як змінилися кутова швидкість і кінетична енергія обертального руху корабля?

9. По похилій площині, висота якої 1 м, першого разу зісковзує без тертя вантаж, наступного разу — скочується без тертя обруч. Маси вантажу та обруча однакові й дорівнюють 1 кг. Радіус обруча — 10 см. Маса обруча розподілена по ободу. Яку швидкість поступального руху матимуть вантаж та обруч після спуску з похилої площини?

10. На обід шківа, насадженого на спільну вісь із маховим колесом, намотано нитку, до кінця якої підвішений вантаж масою 1 кг. На яку відстань має опуститися

вантаж, щоб махове колесо зі шківом отримало кутову швидкість

Момент

інерції колеса зі шківом — 0,39 кг · м², радіус шківа — 0,1 м.

11. Тіло кинули зі швидкістю v₀ під кутом до горизонту. Визначте швидкість тіла на висоті

 

 

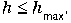
Це матеріал з підручника Фізика і астрономія за 10 клас Засєкіна (профільний рівень)