Попередня сторінка: 2.1 Методика навчання нумерації чисел т...
Наступна сторінка: 2.2.2. Методика вивчення додавання і від�...
2.2.
ЧИСЛА 11-100
2.2.1. Нумерація чисел 11-100
Очікувані результати навчання здобувачів освіти див. на сайті interactive.ranok.com.ua.

Наочні посібники і дидактичний матеріал:
• арифметичні штанги;
• кружки-намистинки;
• площинка «Сотня»;
• картки з одноцифровими і круглими числами;
• лічильні палички;
• лічильний матеріал;
• таблиця чисел «Сотня».
МЕТОДИКА ВИВЧЕННЯ ОКРЕМИХ ПИТАНЬ ТЕМИ
Традиційно нумерацію в межах 100 було поділено на два етапи: числа 11-20 та числа 21-100. Такий порядок вивчення обумовлений тим, що лише для чисел 11-19 порядок назви розрядних чисел, що їх складають, і порядок запису не збігаються: 12 — дванадцять — спочатку називаємо одиниці, а потім десятки, а пишемо першим 1 десяток і лише потім 2 одиниці. 21 — двадцять один — порядок читання і запису збігаються.
Але разом із тим нумерація двоцифрових чисел до і після 20 принципово схожа: усна і письмова нумерація цих чисел спирається на десяткове групування одиниць при лічбі і на позиційний принцип запису числа, десяткову систему числення. Отже, немає сенсу вивчати «два рази» один і той самий матеріал, тим більше, що діти приходять до школи вже зі знанням назв чисел у межах 100. Тому в програмі з математики, починаючи з 2011 року, не виділяються ці два етапи, а пропонується вже в 1 класі вивчити нумерацію чисел у межах 100. Однак, взявши до уваги відмінність у порядку читання і запису чисел 11-19, автори підручників математики НУШ спочатку пропонують розглядати числа 11-20, і лише після цього вводять числа 21-100.
Узагальнення різних методичних підходів свідчить, що вивчення нумерації чисел у будь-якому концентрі ділиться на два етапи: 1) вивчення усної нумерації; 2) вивчення письмової нумерації.
При вивченні нумерації чисел першого десятка усна і письмова нумерація вивчаються паралельно. При вивченні нумерації чисел 11-100 усна і письмова нумерація розглядаються окремо.
Формування поняття про десяток як складену лічильну одиницю
Лічба пар, трійок, п’ятірок... предметів
Вивчаючи числа першого десятка, доцільно лічити двійками, трійками, п’ятірками...
Вчитель пропонує полічити, скільки учнів сидять за однією партою. [Двоє, два, пара.]
Далі учні рахують, скільки пар учнів сидіть у ряді. [5 пар учнів.]
З’ясовуємо, окремо учнів тут більше чи менше, ніж 5 пар.
Після виконання вправ на лічбу групами учні роблять висновок: вміючи лічити до 10, можна полічити велику кількість предметів, якщо їх згрупувати.
Утворення десятка
Формування поняття про десяток здійснюється засобом зв’язування десяти лічильних паличок у пучок або десяти намисти-нок-одиниць у низку-десяток.
Учням пропонується відрахувати 10 лічильних паличок і назвати, скільки паличок вони відрахували. [Десять паличок.] Учитель повідомляє, що якщо зв’язати їх у пучок, то можна сказати також «десяток паличок». Діти показують десяток паличок і з’ясовують, що в десятку 10 окремих лічильних паличок.
Аналогічно можна працювати з кубиками і бруском кубиків, кружками-намистинками.
Вправи з лічби десятками
Вчитель звертає увагу учнів на те, що вони вже вміють лічити парами, трійками, п’ятірками тощо. Вчитель ставить проблемне запитання: «якщо треба порахувати дуже велику кількість предметів, як це зробити?» [Можна їх згрупувати в десятки.] Таким чином, будемо рахувати десятками. Але спочатку згадаємо, як йдуть числа від 1 до 10, і запишемо їх у порядку зростання на дошці. Тепер полічимо десятками. Учитель бере 1 десяток, 2 десятки, 3 десятки... (учні коментують, скільки десятків він узяв); на дошці записуємо результати лічби.
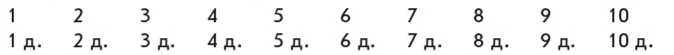
Порівнюємо числа, записані у верхньому та нижньому рядках. Як лічили у верхньому рядку? [Одиницями.] А в нижньому рядку? [Десятками.]
З’ясовуємо, чим відрізняються ці ряди чисел. [У верхньому рядку лічили одиниці, а в нижньому — десятки.]
Визначаємо, чим схожі ці ряди чисел. [У кожному рядку числа записані по порядку від 1 до 10 одиниць; від 1 до 10 десятків.] Доходимо висновку про те, як лічити десятками.

Десять лічильних паличок — це 1 десяток паличок. Пропонуємо учням обміркувати, чи можна вважати, що 1 десяток і 1 одиниця це одне й те саме? [Ні, 1 десяток і 1 одиниця — це не одне і те саме, тому що 1 десяток лічильних паличок містить 10 окремих лічильних паличок.]
Повертаємось до аналізу двох рядків чисел; визначаємо, на скільки кожне наступне число більше у верхньому рядку [на 1 одиницю]; у нижньому [на 1 десяток]. На скільки менше кожне попереднє число у верхньому рядку? [На 1 одиницю.] А в нижньому? [На 1 десяток.]
Далі вчитель бере кілька десятків лічильних паличок і просить назвати, скільки десятків у нього в руці; потім пропонує кільком учням підняти свої десятки лічильних паличок, а клас лічить, скільки десятків лічильних паличок у них є.
Учитель виставляє на наборному полотні геометричні фігури по 10 або предметні картки з десятками предметів і пропонує учням полічити, скільки десятків предметів виставлено.
З’ясовуємо, що вжитті лічать десятками. [Яйця, ґудзики тощо.]
Порівняння чисел, отриманих при лічбі десятками
Учитель бере по кілька десятків лічильних паличок у ліву та праву руки та пропонує порахувати кількість десятків у кожній руці, а потім порівняти, де десятків більше, а де менше. Аналогічне завдання можна запропонувати із застосуванням круж-ків-намистинок, а також набірного полотна і набору (по 10 штук) геометричних фігур або предметних картинок.
Можна провести паралелі між порівнянням одиниць і десятків. Наприклад, можна запропонувати учням покласти 4 окремі намистинки-одиниці ліворуч і 6 намистинок-одиниць праворуч; позначити карками числа та порівняти їх. Потім під ними покласти відповідно 4 низки-десятки намистинок ліворуч та 6 низок-де-сятків намистинок праворуч; позначити числа картками і порівняти одержані числа.
Виконуючи подібні вправи, учні доходять висновку про те, що числа десятків порівнюють так само як і числа одиниць.
Далі можна запропонувати порівняти пари чисел, поданих в одиницях та в десятках. Наприклад: «Порівняйте числа. Що спільне в кожному стовпчику?» [У кожному стовпчику однакові числа, але у верхньому рядку це числа одиниць, а в нижньому — десятків. Спочатку порівнюються одиниці, а потім порівнюються десятки.] З’ясовуємо, чи допоможе результат порівняння чисел у верхньому рядку поставити знак між числами в нижньому рядку? [Так.]
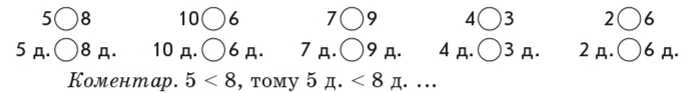
Додавання та віднімання чисел, отриманих при лічбі десятками
Пропонуємо учням практичну роботу з математичними матеріалами (лічильними паличками або кружками-намистинками).
Учитель пропонує учням покласти на парті зліва 2, а справа З намистинки-одиниці; об’єднати їх. Вчитель пропонує пригадати, що значить об’єднати [об’єднати — це означає додати]; визначити, скільки всього одиниць; записати рівність.
Вчитель пропонує покласти зліва 2 низки-десятки, а справа З низки-десятки; об’єднати їх; визначити, скільки всього десятків; записати рівність.
Зіставляємо одержані рівності й доходимо висновку, що числа десятків додають так само, як і числа одиниць.
Аналогічно вводимо віднімання чисел десятків.
Учитель пропонує учням покласти на парті 7 намистинок-одиниць, вилучити 4 намистинки-одиниці. Вчитель пропонує пригадати, що значить вилучити. [Вилучити — це значить відняти.] З’ясовуємо, скільки залишилося одиниць; записуємо рівність.
Учитель пропонує учням покласти на парті 7 десятків, вилучити 4 десятки. З’ясовуємо, скільки залишилося десятків; записуємо рівність.
Зіставляємо одержані рівності й доходимо висновку про те, що числа десятків віднімають так само, як і числа одиниць.
Від практичних дій переходимо до виконання аналогічних завдань за малюнками, наприклад: «Прокоментуйте малюнок і складіть за ним рівність.»
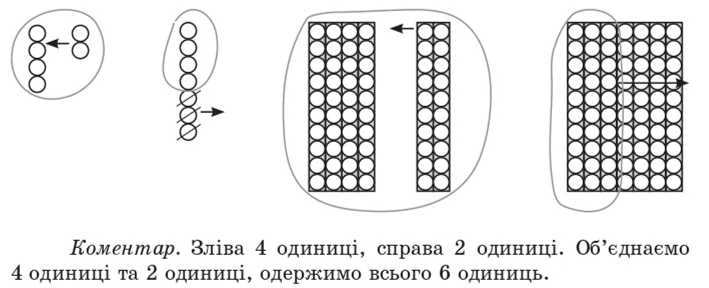
Об’єднати — означає додати, тому складаємо рівність на додавання: 4 + 2 = 6.
Об’єднали 4 десятки та 2 десятки, одержали 6 десятків.
Об’єднати — означає додати: 4 д.+ 2 д. = 6 д.
Було 7 одиниць, вилучили 3 одиниці, залишилося 4 одиниці. Вилучити — означає відняти: 7-4 = 3.
Було 7 десятків, вилучили 3 десятка, залишилось 4 десятки. Вилучити — означає відняти. 7 д.-4 д. = 3 д.
Далі пропонуємо завдання без унаочнення, але додавання та віднімання чисел десятків подається у співставленні із додаванням та відніманням відповідних чисел одиниць, наприклад: «Порівняйте вирази в кожному стовпчику. Чи допоможе вираз у верхньому рядку знайти значення виразу в нижньому рядку?» [Так, допоможе.]

Коментар. Від 8 відняти 5 буде 3. Від 8 десятків відняти 5 десятків також буде 3, але десятків, тому що ми виконуємо дії з десятками.
До 2 додати 7 буде 9. До 2 десятків додати 7 десятків, також буде 9, але не одиниць, а десятків; ми додаємо десятки й одержуємо десятки.
Робимо висновок:
|
Десятки додають і віднімають так само, як і одиниці. |
Після проведеної роботи можна очікувати, що додавання і віднімання чисел, поданих у десятках, не викличе в дітей труднощів: «Знайдіть значення виразів.»

Коментар. До 5 десятків додаємо 3 десятки; десятки додають так само, як і прості одиниці, але в результаті одержують десятки; 5 + 3 = 8; 5 д. + З д. = 8 д...
Тепер у завдання для формування вміння порівнювати математичний вираз і число або математичні вирази можна включати числа, подані в десятках, наприклад: «Порівняйте математичний вираз і число або математичні вирази.»

Коментар. Треба порівняти суму 5 десятків і 2 десятків з числом 8 десятків; знаходимо значення суми: 5 д.+ 2 д. = 7 д.; порівнюємо числа: 7 д. < 8 д., тому між сумою і числом ставимо такий самий знак: сума чисел 5 д. і 2 д. менша від 8 д.
Треба порівняти число 4 десятки з різницею 9 десятків і 6 десятків. Знаходимо значення різниці: 9 д.-б д. = 3 д.; порівнюємо числа: 4 д. > 3 д.; ставимо такий самий знак між числом і виразом: 4 д. > 9 д. - 6 д. — 4 десятки більше за різницю 9 десятків і 6 десятків.
Треба порівняти суму 5 десятків і 4 десятків із сумою З десятків і 7 десятків. Знаходимо значення кожного виразу: 5 д. + 4 д. = 9 д., З д. + 7 д. = 10 д.; порівнюємо числа: 9 д. < 10 д., тому сума чисел 5 десятків і 4 десятків менша від суми чисел 3 десятків та 7 десятків.
Поняття про одноцифрові і двоцифрові числа
Учням пропонується записати числа від 0 до 10, уважно розглянути ці числа і встановити, яке число тут «зайве». Учні з’ясовують, що зайве число 10, тому що решту чисел записують лише однією цифрою, а число 10 — двома цифрами. Учитель вилучає число 10 і пропонує учням встановити, яка спільна ознака притаманна всім цим числам. Учні називають: запис за допомогою однієї цифри. Можна запропонувати дітям дати назву числам, у яких істотна ознака — запис однією цифрою. Числа, що записують за допомогою однієї цифри, називають одноцифровими.
Далі з’ясовуємо, скількома цифрами записують число 10. [Двома.] Учитель пропонує учням дати назву цьому числу за аналогією. Учні міркують так: якщо число, яке записують однією цифрою, називають одноцифровим, то число, яке записують двома цифрами, можна назвати двоцифровим. З метою випереджального навчання можна запропонувати дати назви чисел, які записують трьома, чотирма, п’ятьма... цифрами.
З’ясування значення цифр у записі числа 10
Учні викладають на парту 10 лічильних паличок, збирають їх разом і зв’язують у пучок, таким чином одержують 1 десяток паличок або викладають 10 намистинок-одиниць одна під одною та замінюють їх низкою-десятком. Записуємо число 10:

Діти з’ясовують, яка цифра в записі показує, що в цьому числі 1 десяток; підкреслюють цю цифру. Визначаємо, на якому місці вона стоїть (на першому місці, рахуючи зліва направо). Далі встановлюємо, що показує в числі 10 цифра 0 (цифра 0 показує, що всі палички або намистинки зв’язані і вільних немає).
Беремо 2 десятки лічильних паличок. Ставимо запитання: «Як записати це число? На якому місці ми запишемо, що тут 2 десятки?» [На першому місці.] «А як ми запишемо, що всі десятки зв’язані в пучки і немає вільних паличок?» [Ми запишемо на другому місці цифру 0.]
Аналогічним чином працюємо над записом інших чисел десятків:
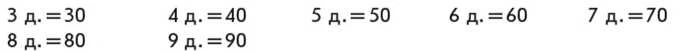
Читаємо числа: 1 десяток — десять; 2 десятки — двадцять (складається з двох частин: «два-» — кількість десятків і «-дцять» — скорочено «десять»); 3 десятки — тридцять; 4 десятки — сорок (цю назву треба запам’ятати); 5 десятків — п’ятдесят. Як назвати число 6 десятків? [Шістдесят.] Як назвати 7 десятків? [Сімдесят.] Як назвати 8 десятків? [Вісімдесят.] 9 десятків — дев’яносто (це треба запам’ятати).

З’ясовуємо, назви яких чисел схожі. Чим схожі? Пропонуємо учням знайти числа, назви яких відрізняються від решти, записати їх.
На наступному етапі читаємо круглі числа, визначаючи кількість десятків, що в них містяться, та записуємо круглі числа від 10 до 90, рахуючи десятками: 10, 20, 30, 40, 50, 60, 70, 80, 90.
Порівняння круглих чисел
З метою перенесення учнями відомого способу дії доцільно подавати у співставленні круглі числа з відповідними числами десятків, наприклад, пропонуємо учням порівняти записи чисел у верхньому та нижньому рядках кожного стовпчика; з’ясувати, що в них спільне. [Це одні й ті самі числа, але у верхньому рядку числа записані у десятках, а в нижньому — як круглі числа — в одиницях] Пропонуємо порівняти числа у верхньому рядку, з’ясувати, чи допоможе це порівняти числа у нижньому рядку. [Так, бо це одні й ті самі числа.]
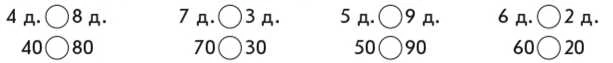
Коментар. 4 десятки менше від 8 десятків, тому 40 менше від 80...
З’ясовуємо, як можна міркувати при порівнянні круглих чисел. [Треба круглі числа замінити десятками, порівняти числа десятків і поставити такий самий знак між круглими числами.] Далі, пропонуючи учням для порівняння круглі числа, наприклад:

Коментар. 70 — це 7 десятків, 50 — це 5 десятків; 7 десятків більше за 5 десятків, тому 70 більше за 50...
Додавання і віднімання круглих чисел
Учні вже набули досвіду додавання та віднімання чисел, поданих у десятках, тому при введенні додавання і віднімання круглих чисел доцільно спиратися на це вміння. Так, додавання і віднімання круглих чисел подаємо у співставленні з додаванням та відніманням відповідних чисел, поданих у десятках. Наприклад, пропонуємо учням порівняти записи чисел у верхньому та нижньому рядках кожного стовпчика; з’ясувати, що в них спільне. [Записані одні й ті самі числа, але у верхньому рядку вони подані в десятках, а в нижньому — в одиницях.] Пропонуємо учням знайти значення виразів у верхньому рядку, з’ясувати, чи допоможуть вони знайти значення виразів у нижньому рядку. [Так, бо додають або віднімають одні й ті самі числа.]

Коментар. До 4 десятків додати 2 десятки одержимо 6 десятків; тому до 40 додати 20 — це 4 десятки плюс 2 десятки буде 6 десятків, або 60...
Аналізуючи власні дії, учні доходять висновку про те, як можна міркувати при додаванні або відніманні круглих чисел; чим їх можна замінити.
Пропонуємо учням виконати арифметичні дії над круглими числами, замінюючи їх десятками.

Коментар. Від 70 треба відняти 40; замінюємо 70 на 7 десятків, 40 — на 4 десятки; віднімаємо числа десятків — 7 десятків мінус 4 десятки буде 3 десятки, або 30...
До ЗО треба додати 50; замінюємо 30 десятками — буде 3 десятки; замінюємо 50 десятками — 5 десятків; додаємо числа десятків — 3 десятки плюс 5 десятків буде 8 десятків, або 80.
УТВОРЕННЯ ЧИСЕЛ ВІД 11 ДО 20.
УСНА НУМЕРАЦІЯ
Під час вивчення усної нумерації показуємо учням утворення чисел від 11 до 20 — прираховуючи по 1, показуємо, що числа 11-20 можуть бути утворені приєднанням 1, 2, 3, ... до 10, при цьому необхідно підкреслити характер дії (покласти 1 на 10, 2 на 10 тощо) і пов’язати з цим пояснення назв чисел другого десятка. Прираховуючи числа по 1, підкреслюємо тим самим, що за межами десятка числа так само упорядковані, як і в межах 10. Для засвоєння десяткового складу числа застосовуються вправи двох видів: утворення числа із 1 десятка і кількох одиниць та розкладання числа на десятки й одиниці.
Одержання чисел другого десятка. Десятковий склад чисел другого десятка
Пропонуємо учням практичну роботу з математичним матеріалом з утворення чисел від 11 до 20.
Відрахуйте 10 лічильних паличок; зв’яжіть їх у пучок. Як сказати інакше, скільки у вас паличок? [1 десяток.] Візьміть 1 паличку, покладіть її на десяток. Що ми зробили? [Ми 1 поклали на 10.] Скільки стало всього паличок? [Один-на-дцять.] Ми отримали число 11. Хто помітив зв’язок між дією, що ми виконували над десятком та одиницею, і назвою отриманого числа? [Ми один поклали на десять. Десять скорочено — «-дцять». Ми один поклали на «-дцять» — один-на-дцять.]
Скільки тут десятків паличок? Візьміть десяток у ліву руку і покажіть. Скільки тут окремих одиниць. Покажіть їх, візьміть їх у праву руку. Скільки десятків і скільки одиниць містить число 11?
Покладіть на десяток ще 1 паличку. Скільки тепер паличок лежить на десятку? [2.] Що ми зробили? [Ми 2 поклали на 10.] Скільки всього паличок? [Два-на-десять — дванадцять.] Скільки десятків у числі 12? Скільки окремих паличок? Скільки десятків і скільки одиниць у числі 12?
Аналогічно розглядаються решта чисел другого десятка, після чого треба звернути увагу учнів на те, що в назвах чисел від 11 до 20 перша частина слова позначає число одиниць, а друга частина «-дцять» указує на 1 десяток, який містить дане число.
Для практичної роботи можна використовувати арифметичні штанги, накладаючи на штангу 10 штанги від 1 до 9. Це завдання дає можливість також поєднати назви чисел із характером виконуваних дій.
Після практичних вправ переходимо до коментування рисунків. Наприклад:
Коментар. На штангу 10 поклали штангу 1. Ми 1 поклали на 10. Одержали 11.

Приставимо 1 до 10 — число 11 більше за 10. Розгляньте, як цю дію виконали з картками з числами. Картку 1 поклали на картку 10, причому її поклали на 0. Тепер не всі одиниці зв’язані у десяток — є ще 1 окрема одиниця. Цифра 1, що записана зліва, означає, що в числі 11 — 1 десяток. Покажіть, яка штанга позначає десяток. Цифра 1 на другому місці означає, що в числі 11 — 1 одиниця. Покажіть, яка штанга позначає одиниці. Прокоментуйте, як одержали інші числа.

Коментар. Ми штангу 2 поклали на штангу 10; ми два поклали на «-дцять», одержали дванадцять. Приставляємо штангу 2 до штанги 10, бачимо, що число 12 більше за 10 і 12 більше за 11. Розглядаємо, як цю дію виконали з картками з числами: 2 поклали на 10, причому картку з числом 2 поклали на цифру 0. Цифра 1 означає, що в числі 12 — 1 десяток. Покажіть штангу, яка позначає десяток. Цифра 2 означає, що в числі 12 — 2 одиниці. Покажіть штангу, яка позначає 2 одиниці.
Після одержання чисел другого десятка та з’ясування їх назв та десяткового складу виконуємо практичні дії зі штангами та картками з числами:
• Складіть за допомогою штанг число, яке містить 1 десяток та З одиниці; позначте його картками з числами.
• Складіть за допомогою штанг число, яке містить 1 десяток та 7 одиниць; позначте його картками з числами.
Читаємо назви чисел:

Пропонуємо учням прочитати окремо виділені частини слів (-дцять). Що цікаве можна помітити? [Ця частина слова в усіх назвах однакова.] Встановлюємо, чому виділена частина слів у всіх словах одна й та сама. [Тому що всі ці числа одержані в результаті прикладання на десяток кількох одиниць. Усі вони містять 1 десяток.] Визначаємо, скільки десятків у кожному числі. [Усі числа містять 1 десяток.] Пропонуємо учням прочитати частини слів, які підкреслено (один, два, три...) й з’ясувати, з якими словами вони зв’язані. [Вони зв’язані з назвами одноцифрових чисел.] У результаті учні доходять висновку про те, що назви чисел другого десятка пов’язані з характером дії, яку виконують при одержанні цих чисел: на десяток накладають певне число одиниць: один-на-дцять; два-на-дцять... Перша частина цих слів означає, скільки одиниць поклали на десяток. А остання частина означає 1 десяток.
Для виконання практичних вправ можна використовувати кружки-намистинки. Наприклад, викладаємо на парті 1 низку-де-сяток і кілька намистинок-одиниць; вчимо учнів позначити число картками з числами. Для цього використовуємо набір карток: картка з числом 10 та картки з числами від 1 до 9. Наприклад:
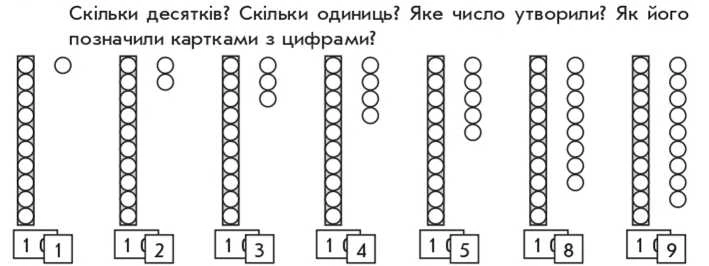
Коментар. Справа від низки-десятка поклали 1 окрему намистинку-одиницю. Маємо 1 десяток та 1 одиницю. Утворили число 11. Щоб його позначити картками, треба на картку 10 покласти картку 1, причому число 1 покласти на цифру 0; тепер не всі одиниці зв’язані в десяток — є 1 окрема одиниця...
Очевидно, що після того як учні набули досвід позначення чисел подібним чином, їм легко буде зрозуміти спосіб одержання чисел другого десятка. Наприклад:
Як одержати число 11? Яку арифметичну дію слід виконати? Як одержати решту чисел?


Коментар. Щоб одержати число 11, треба до 1 десятка приєднати 1 одиницю. Об’єднати — це означає додати. Щоб одержати число 11, треба до 10 додати 1, одержимо 1 десяток і 1 одиницю — 11...
Ознайомлюємо учнів із назвами розрядів
Двоцифрові числа записують за допомогою тих самих цифр, що й одноцифрові числа. Які цифри ви знаєте? [0, 1, 2, 3, 4, 5, 6, 7, 8, 9.] Але при записі двоцифрових чисел має значення місце, на якому записана цифра: цифра, яка стоїть на першому місці зліва, означає десятки, а цифра, яка стоїть на другому місці, — одиниці.

Читаємо кожне число. Скільки в ньому десятків? На якому місці записуються десятки? Скільки в числі одиниць? На якому місці записуються одиниці?
|
Десятки та одиниці називають розрядами. Перший розряд справа — розряд одиниць, другий розряд справа — розряд десятків. |
УТВОРЕННЯ ЧИСЕЛ ВІД 21 ДО 100.
УСНА НУМЕРАЦІЯ
Утворення чисел від 21 до 100
Переносимо одержані знання та вміння на числа в межах 100. Наприклад, учні викладають на парту 1 низку-десяток та 3 намистинки-одиниці й позначають число картками з числами. Далі приєднуємо до десятків по одному десятку й позначаємо одержане число картками з числами та читаємо їх. Наприклад: Скільки десятків? Скільки одиниць? Як позначити число за допомогою карток з числами? Прочитайте одержані числа.
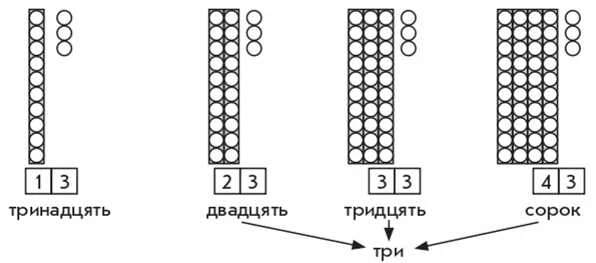
Коментар. Число 13 містить 1 десяток і 3 одиниці; щоб позначити це число, треба на картку з числом 10, на цифру 0, покласти картку з числом 3 — отримаємо число тринадцять.
Число 23 містить 2 десятки та 3 одиниці; щоб позначити це число, треба взяти картку з числом 20 і на цифру 0 покласти картку з числом 3 — це число читають так: спочатку називають десятки «двадцять», а потім одиниці «три» — двадцять три...
Записуємо в рядок отримані числа. З’ясовуємо, на скільки кожне наступне число в цьому ряду більше за попереднє [на 10]; на скільки попереднє число менше від наступного [на 10].
У результаті власної діяльності учні доходять висновку: щоб одержати двоцифрові числа, можна до кількох десятків приєднати кілька одиниць.
Читання чисел
Пропонуємо багато вправ на читання чисел, які проілюстровані лічильними паличками. Учні повинні не тільки назвати відповідне число, а визначити його десятковий склад. Наприклад: на рисунку 4 десятки паличок і 2 окремі палички — це 4 десятки та 2 одиниці; 4 десятки та 2 одиниці складають число 42. Ілюструємо число за допомогою намистинок-одиниць та низок-десятків, визначаємо його десятковий склад та читаємо відповідне число. При читанні чисел від 21 до 100 спочатку називаємо число десятків, а потім число одиниць. Наприклад:
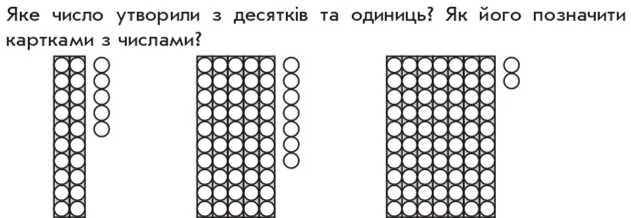
Коментар. У числі 2 десятки, тому покладемо картку «20», і 5 одиниць, тому покладемо картку «5» на нуль — 25. Читаємо число: перша частина слова означає, що в ньому 2 десятки, а друга — що в ньому 5 одиниць — двадцять п’ять...
Якщо в учнів є набори кружків-намистинок, то виконуємо практичні вправи типу: «Покладіть 4 десятки і 6 одиниць. Позначте картками число, яке одержали. Прочитайте його...».
Пропонуємо учням завдання на читання чисел без унаочнення. Спочатку учні читають числа, записані в розрядній таблиці, а потім і без розрядної таблиці. Наприклад: прочитати числа 56, 34... Тут учні спочатку визначають число десятків та число одиниць і лише потім використовують спосіб називання таких чисел. На-прикла: вчитель пропонує з’ясувати, що означає цифра, яка стоїть на першому зліва місці в записі двоцифрового числа [десятки]; на другому місці [одиниці]. Пропонує прочитати числа, визначаючи, скільки в числі десятків, скільки одиниць.

Коментар. У першому числі 5 десятків і 9 одиниць. Спочатку називаємо десятки — п’ятдесят, а потім одиниці — дев’ять; п’ятдесят дев’ять. У числі 59 п’ять десятків та дев’ять одиниць... Корисними будуть вправи із таблицею чисел «Сотня»:
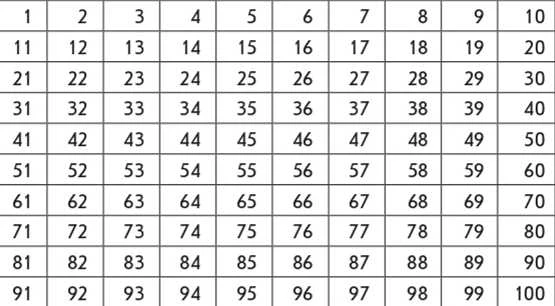
Читаємо числа першого рядка. Це одноцифрові числа, бо вони містять лише одиниці. Читаємо числа другого рядка і визначаємо їх вид (двоцифрові). З’ясовуємо, що в записі цих чисел означає цифра на першому місці справа наліво (ця цифра означає одиниці), що означає цифра на другому місці справа (десятки).
Читаючи числа третього рядка, треба до слова «двадцять» (так читається відповідне кругле число) додати кілька одиниць.
Корисно поставити такі запитання:
Прочитайте числа четвертого рядка.
Яке спільне слово містять назви чисел п'ятого рядка? [«Сорок».] Прочитайте числа п'ятого рядка.
Які числа мають стояти в шостому рядку?..
Доцільними будуть вправи на співставлення чисел, які записані однаковими цифрами, що розташовані на різних місцях:

З’ясовуємо, що спільне в кожній парі чисел. [Кожну пару чисел записують однаковими цифрами.] Чим вони відрізняються? [Порядком запису цифр.] Обмірковуємо, чим відрізняються назви чисел, у яких 1 десяток, від назв інших двоцифрових чисел. [Числа, у яких 1 десяток, закінчуються на «-дцять», що і позначає в них 1 десяток, а починаються з числа одиниць. Назви інших двоцифрових чисел починаються з числа десятків і закінчуються числом одиниць.]
Послідовність чисел у межах 100 в натуральному ряді Учні мають навчитися лічити в межах 100 в прямому і зворотному порядку, визначати місце числа в натуральному ряді: називати попереднє і наступне числа. З цією метою знайомимо учнів із таблицею чисел «Сотня» і пропонуємо їм такі завдання.
Назвіть числа 3-го десятка. [21, 22, 23, 24, 25, 26, 27, 28, 29, ЗО.] Яким числом закінчується даний десяток? [ЗО] 3 якого числа починається? [21] Що спільне в чисел третього десятка? [Усі числа, крім ЗО, містять по 2 десятки.] Чим вони відрізняються? [Одиницями.] На скільки кожне наступне число більше за попереднє? [На 1.] На скільки попереднє менше? [На 1.]
Прочитайте числа четвертого стовпчика. [4, 14, 24, 34, 44, 54, 64, 74, 84, 94.] Що спільне в чисел кожного стовпчика? [Однакові одиниці. Усі ці числа містять по 4 одиниці.] Чим вони відрізняються? [Десятками.] На скільки кожне наступне число стовпчика більше за попереднє? [На 10.] На скільки попереднє число менше? [На 10.] Назвіть усі числа, які містять по 4 десятки. [40, 41, 42, 43, 44, 45, 46, 47, 48, 49.] Чим вони відрізняються? [Одиницями.] Назвіть усі числа, які містять по 4 одиниці. [4, 14, 24, 34, 44, 54, 64, 74, 84, 94.] Чим вони відрізняються? [Десятками.]
Назвіть «сусідів» чисел: 56, 79, 31. [«Сусіди» числа 56: наступне число 57, попереднє число 55.] Назвіть попереднє число до числа 66. Назвіть наступне число за числом 89...
Є сенс проілюструвати послідовність чисел на числовому промені.

Пропонуємо учням прочитати одноцифрові числа [0, 1, 2, З, 4, 5, 6, 7, 8, 9]; двоцифрові числа [10, 11, 12,13, 14, 15, 16...]; назвати найменше одноцифрове число [0]; найбільше одноцифрове число [9]. З’ясувати, яке число йде за найбільшим одноцифровим числом. [За найбільшим одноцифровим числом йде найменше двоцифрове число.]
Спосіб утворення чисел
Тут застосовуються такі способи утворення чисел: 1) з кількох десятків та кількох одиниць [54 утворюється з 5 десятків та 4 одиниць]; 2) додаванням 1 до попереднього числа [54 утворюється додаванням 1 до попереднього числа 53]; 3) відніманням 1 від наступного [54 утворюється відніманням 1 від наступного числа 55].
ПИСЬМОВА НУМЕРАЦІЯ
Запис чисел другого десятка
Використовуючи абак, пучки лічильних паличок та окремі палички або застосовуючи низки-десятки і окремі намистинки-одиниці та картки з круглими й одноцифровими числами, позначаємо картками числа другого десятка. Наприклад, розкладено 13 лічильних паличок: 1 пучок — десяток та 3 окремі палички — одиниці. Учні визначають десятковий склад числа 13 та позначають його картками в нижніх кишенях абака.
У математичних матеріалах М. Монтессорі є дошки Сегена для позначення і читання чисел другого десятка. Можна запропонувати учням розглянути цю дошку і з’ясувати, що на ній записано одне й те саме число 10 дев’ять разів. Потім учні на нуль накладають картки з одноцифровими числами від 1 до 9 і читають одержані числа. Обговорюємо, що зробили з цією дошкою. [На нуль поклали картку з числом одиниць.] Читаючи одержані числа, звертаємо увагу учнів на те, що означає перша частина цього слова [скільки одиниць у числі]; що означає друга частина слова [що ці одиниці поклали на десяток, тобто скільки десятків у цьому числі]; з’ясовуємо, скільки в кожному числі десятків [1 десяток]; скільки одиниць [1 одиниця, 2 одиниці...]. Визначаємо, на якому
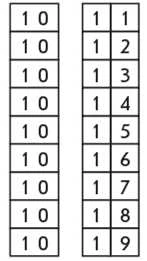
місці зліва записані десятки [на першому]; на якому місці записані одиниці [на другому].
Далі пропонуємо учням прочитати числа, записані в розрядній таблиці.
17... На якому місці записуються десятки? [На першому місці зліва.] На якому місці записуються одиниці? [На другому місці.]
Переходимо до запису чисел у нумераційній таблиці. Спочатку зазначаємо розрядний склад числа, наприклад: 1 десяток і 5 одиниць; 1 десяток і 8 одиниць; 1 десяток і 1 одиниця; 1 десяток і 7 одиниць; 1 десяток; 1 десяток і 2 одиниці; 7 одиниць; 1 десяток і 9 одиниць. А потім записуємо числа без визначення розрядного складу: 13, 16, 5, 14.
Запис чисел у межах 21—100
Спираємося на вміння учнів записувати числа другого десятка (на першому місці справа наліво пишуть одиниці, а на другому — десятки) та на знання десяткового складу чисел першої сотні.
Використовуючи абак, пучки лічильних паличок та окремі палички, повторюємо письмову нумерацію чисел другого десятка. Наприклад, на абаку розкладено 13 лічильних паличок: 1 пучок — десяток та 3 окремі палички — одиниці. Учні визначають десятковий склад числа 13 та позначають його картками в нижніх кишенях абака. Далі беремо ще 1 пучок-десяток та кладемо у відповідну кишеню: тепер у розряді десятків 2 десятки, отже, змінюємо картку, що позначає десятки, і т. д. Робимо висновок: у двоцифрових числах на першому місці справа наліво пишемо одиниці, а на другому — десятки.

Навчання молодших школярів запису чисел першої сотні здійснюється за допомогою спеціальних завдань.
Використовуючи математичні матеріали М. Монтессорі — дошку Сегена, можна запропонувати учням завдання.
Пропонуємо учням уважно розглянути дошку; прочитати записані числа; з’ясувати, що можна про них сказати. [Це круглі десятки.] Пропонуємо розглянути картки з цифрами від 1 до 9.
Картки з цифрами 1, 2, 9 накладатимемо на 10.
1 (2, 3...) покладемо на 10. З’ясовуємо, яке число ми одержимо. Скільки в цьому числі десятків? скільки одиниць? Зверніть увагу: після того як на 10 покладемо картку 9, ми переходимо до наступного рядка. Тепер на 20 накладатимемо картки з цифрами від 1 до 9. Накладаючи, називаємо одержані числа. Читаємо числа, складені на дошці.
Перед записом чисел пропонуємо учням розглянути, як записали числа в нумераційній таблиці, і прочитати ці числа.
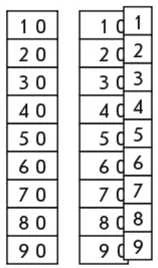
А потім пропонуємо учням записати в нумераційній таблиці числа, у яких: 1 десяток і 7 одиниць; 7 десятків і 7 одиниць; 5 десятків; 4 десятки і 3 одиниці; 7 одиниць; 6 десятків.
Далі учні в зошиті записують числа за розрядним складом: 5 десятків 4 одиниці; 8 десятків 1 одиниця.
Врешті, учні в зошитах записують числа без вказаного розрядного складу, наприклад: двадцять вісім, п’ятнадцять, сорок три.
Також засвоєнню нумерації двоцифрових чисел сприяють вправи:
1) поясніть, що означає кожна цифра в записі числа (наприклад, у числі 47 цифра 7 означає кількість одиниць, а цифра 4 — кількість десятків);
2) запишіть за допомогою даних цифр можливі двоцифрові числа (наприклад, з цифр 2 та 5 можна скласти такі двоцифрові числа: 22, 25, 52, 55);
3) дайте характеристику числу: десятковий склад, місце в натуральному ряді, особливості запису (наприклад, число 43 містить 4 десятки та 3 одиниці; попереднє до нього число 42, а наступне — 44; це двоцифрове число записують за допомогою двох різних цифр: 4 та 3).
Запис числа у вигляді суми розрядних доданків Після того як діти навчаться визначати десятковий склад та записувати двоцифрові числа, вводиться поняття «сума розрядних доданків» як така сума, у якій десятки та одиниці подано окремо, інакше кажучи, це сума десятків та одиниць.
Щоб подати число у вигляді суми розрядних доданків, треба: 1) визначити кількість десятків (підкреслити десятки в записі числа двома рисками); 2) визначити кількість одиниць (підкреслити одиниці однією рискою); 3) записати десятки у вигляді круглого числа; 4) до круглого числа додати одиниці. Наприклад: 74 = 70+4.
Слід зазначити, що подання числа у вигляді суми розрядних доданків спирається на досвід дітей позначення картками двоцифрових чисел, коли вони на картку з круглим числом накладали картку з одноцифровим числом. У даному випадку дія обернена — тепер ми маємо розсунути ці картки.
Порівняння чисел
На цьому етапі навчання застосовуються такі способи порівняння чисел.
Спосіб на підставі розташування чисел на числовому промені або в натуральному ряді: число, яке на числовому промені розташовується праворуч або яке при лічбі називають пізніше, більше, а число, що на числовому промені розташовується ліворуч або при лічбі називають раніше, менше.
З цим способом порівняння діти вже добре знайомі: ознайомлення з ним відбулося при вивченні порівняння чисел першого десятка, а закріплення відбувається при вивченні порівняння чисел до 20. Тому на етапі актуалізації слід повторити, як треба міркувати при порівнянні чисел першого десятка; а потім запитати учнів: «Чи можна так само міркувати при порівнянні чисел від 11 до 20? при порівнянні чисел першої сотні?». Отримавши від учнів позитивну відповідь, перенести цей спосіб порівняння в нову ситуацію. Наприклад: «як можна міркувати при порівнянні одноцифрових чисел?» [Можна складати пари, можна порівнювати числа за порядком їх розташування в натуральному ряді, а можна порівнювати логічним способом.] З’ясовуємо, у чому полягає спосіб порівняння за місцем числа в натуральному ряді. [Число, яке йде в натуральному ряді рані-ше/розташовується ліворуч від даного, менше. Число, яке йде в натуральному ряді пізніше/розташовується праворуч від даного, більше.] Пропонуємо учням порівняти числа за місцем розташування в натуральному ряді.

Коментар. Треба порівняти 5 і 8; 5 на числовому промені розташовується ліворуч від 8 або при лічбі йде раніше за 8, тому 5 менше від 8. Треба порівняти 7 і 4; 7 на числовому промені розташовується праворуч від 4 або при лічбі йде пізніше, тому 7 більше 4.
Переносимо спосіб порівняння чисел за розташуванням числа на числовому промені або місцем числа в натуральному ряді на числа в межах 20.
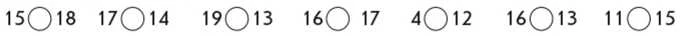
Чи можна так само міркувати при порівнянні двоцифрових чисел? [Так.] Двоцифрових і одноцифрових чисел? [Так.]

Коментар. Треба порівняти числа 14 та 18; 14 розташовується на числовому промені ліворуч або йде в натуральному ряді раніше 18, тому 14 менше 18. Треба порівняти 23 і 32; 23 йде в натуральному ряді при лічбі раніше 32; тому 23 менше 32. Треба порівняти 57 і 51; 57 йде в натуральному ряді при лічбі пізніше числа 51, тому 57 більше 51...
Порівнюючи пари чисел у другому стовпчику, з’ясовуємо, що в натуральному ряді спільне в парах чисел. [До складу кожної пари входять одноцифрове та двоцифрове числа.] Спираючись на результат порівняння, учні роблять висновок:
|
Будь-яке одноцифрове число менше від будь-якого двоцифрового числа. Будь-яке двоцифрове число більше за будь-яке одноцифрове число. |
Корисними будуть вправи: назвіть числа, які менші від числа 16; назвіть двоцифрові числа, які менші від 18; назвіть числа другого десятка, які більші за 12; назвіть числа, які більші за 13, але менші від 16.
Порозрядне порівняння чисел починається з найвищого розряду і відбувається за алгоритмом:
1) підкреслюю число десятків у кожному числі;
2) порівнюю числа десятків: більше те число, у якому десятків більше (менше те число, у якому десятків менше); якщо десятків порівну, то переходжу до п. 3;
3) підкреслюю число одиниць у кожному числі;
4) порівнюю числа одиниць: більше те число, у якому одиниць більше (менше те число, у якому одиниць менше); якщо одиниць порівну, то ці числа рівні.
Наприклад, треба порівняти 27 і 19. У числі 27 — 2 десятки, а в числі 19 — 1 десяток; порівнюємо числа десятків: 2 десятки більше за 1 десяток, тому число 27 більше за 19. Треба порівняти ЗО і 32. У числі ЗО — 3 десятки, у числі 32 — 3 десятки; порівнюємо числа десятків — порівну, тому переходимо до одиниць; у числі ЗО — 0 одиниць, у числі 32 — 2 одиниці; порівнюємо одиниці: 0 менше 2, тому число ЗО менше числа 32...
Це новий спосіб порівняння. Він буде широко застосовуватися при порівнянні чисел у всіх подальших концентрах, тому йому слід приділити певну увагу.
ВИПАДКИ ДОДАВАННЯ І ВІДНІМАННЯ НА ПІДСТАВІ НУМЕРАЦІЇ ЧИСЕЛ
Додавання та віднімання числа 1
Додавання та віднімання числа 1 здійснюється на підставі порядку розташування чисел у натуральному ряді: додати до будь-якого числа 1 — це означає отримати наступне число; відняти від будь-якого числа 1 — це означає отримати попереднє число.
Правило додавання та віднімання числа 1 було засвоєне учнями на попередньому етапі навчання — у концентрі «Десяток», тому в цій темі його слід перенести в нову ситуацію. Спочатку переносимо на випадки додавання та віднімання в межах 20, а потім на числа в межах 100.
Завдання вчителя полягає в тому, щоб учні успішно здійснили перенесення знань у нову ситуацію. Для цього треба актуалізувати порядок розташування чисел до 20 (100); поняття «попереднє» і «наступне» числа; правила додавання і віднімання числа 1 у межах 10. Для полегшення переносу знань у нову ситуацію можна запропонувати учням трійки рівностей, у яких перший доданок або зменшуване відрізняється кількістю десятків. Наприклад:
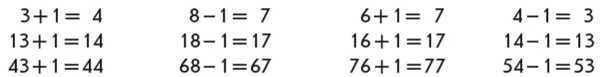
З’ясовуємо, чим схожі вирази кожного стовпчика; чим відрізняються.
Встановлюємо, чи є спільне в способі додавання числа 1; віднімання числа 1.
Який висновок можна зробити?
|
Додати до будь-якого числа 1 — означає отримати наступне |
|
число. Відняти від будь-якого числа 1 — означає отримати |
|
попереднє число. |
Випадки додавання до круглих десятків кількох одиниць. Випадки віднімання від числа або його десятків, або його одиниць Додавання до десятків окремих одиниць
Спочатку опрацьовуємо цей прийом обчислення на прикладі чисел від 11 до 20. Слід зазначити, що тут в нагоді стане
досвід, одержаний при позначенні картками з числами двоцифрових чисел; при заміні числа сумою розрядних доданків. Застосовуємо арифметичні штанги. Наприклад: приєднуємо до штанги «10» штангу «7» («8», «5», ...), одержуємо число 17 (18, 15...). Визначаємо його десятковий склад, позначаємо число картками з цифрами: накладаємо картку «7» («8», «5»...) на картку «10». Ми приєднали штангу «10» і штангу «7» («8», «5»...). Що значить «об’єднати» на математичній мові? [Це значить додати.] Які штанги об’єднали? Подивіться, як склали рівність.

Далі від дії з реальними предметами переходимо до дії зі схемами.

Коментар. До 10 треба додати 7. 10 — це 1 десяток, 7 — це 7 одиниць; поєднуємо: 1 десяток і 7 одиниць складають число 17...
Переносимо розглянутий спосіб міркування на числа від 21 до 100. Наприклад:
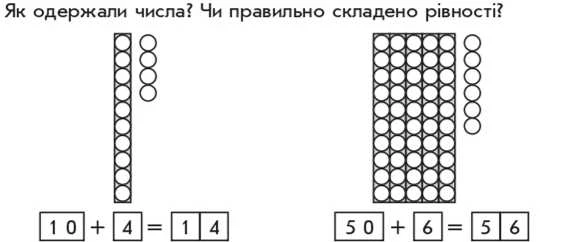
Щоб одержати число 14, ми до 1 десятка приєднали 4 одиниці. Рівність записано правильно: 1 десяток — це 10; до 10 додали — приєднали — 4 одиниці, одержали 14...
Щоб одержати число 56, до 5 десятків приєднали 6 одиниць. Рівність записано правильно: 5 десятків — це 50; до 50 додати — приєднати — 6 одиниць буде 56...
Учні порівнюють рівності. У кожній рівності до круглого числа — до числа десятків — додаємо число одиниць і одержуємо двоцифрове число, яке містить і десятки, і одиниці. Формулюємо пам’ятку:
|
ПАМ’ЯТКА |
|
Додавання на підставі розрядного складу числа |
|
1. Замінюю двоцифрове кругле число десятками. |
|
2. Читаю інший доданок з назвою одиниць. |
|
3. Поєдную десятки з одиницями. |
|
4. Записую число, яке містить дану кількість десятків та |
|
одиниць. |
|
Наприклад: 30+7=3 д. 7 од. = 37 |
Міркуючи за пам’яткою, знаходимо значення сум:

Коментар. 10+5. 10 — це 1 десяток, 5 — це 5 одиниць; об’єдную десятки й одиниці — 1 десяток і 5 одиниць; 1 десяток і 5 одиниць складають число 15.
Ознайомлення учнів зі способом віднімання від двоцифрового числа його одиниць (спосіб віднімання на основі знання розрядного складу числа)
Опрацьовуємо цей спосіб міркування на числах від 11 до 20. Утворюємо за допомогою штанг число 16 (18, 17...). Визначаємо, скільки в ньому десятків; скільки одиниць. Позначаємо одержане число за допомогою карток з цифрами. Відсуваємо штангу «6» («8», «7»...). Відсуваємо картку з цифрою 6 (8, 7...) Визначаємо, що залишилося. Що значить відсунути, вилучити на математичній мові? Подивіться, як складено рівність.

Від практичних дій та розгляду малюнків, які ілюструють віднімання від числа другого десятка його одиниць, переходимо до виконання дії з коментарем, використовуючи схеми. Наприклад:
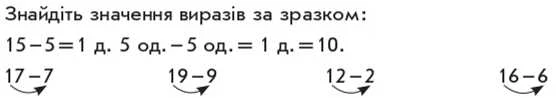
У двоцифрових числах підкресліть одиниці однією рискою, а десятки—двома. В одноцифрових числах підкресліть одиниці однією рискою.
Коментар. 15-5. 15 — це 1 десяток і 5 одиниць; від 1 десятка і 5 одиниць віднімаємо 5 одиниць, залишається 1 десяток, або 10...
Ознайомлення учнів зі способом віднімання від двоцифрового числа його десятків (спосіб віднімання на основі знання розрядного складу числа) відбувається аналогічно.
Утворюємо за допомогою штанг число 14 (15, 19...). З’ясовуємо, скільки в ньому десятків; скільки одиниць. Позначаємо одержане число за допомогою карток з числами. Відсуваємо штангу «10». Відсуваємо картку «10». Визначаємо, що залишилося. Що значить відсунути, вилучити на математичній мові? Подивіться, як складено рівність.

Переходимо до виконання дії за схемами. Наприклад: Знайдіть значення виразів за зразком:
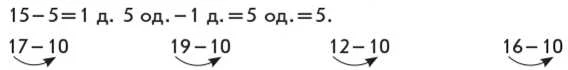
У двоцифрових числах підкресліть одиниці однією рискою, а десятки — двома. В одноцифрових числах підкресліть одиниці однією рискою.
Коментар. 17-10. 17 — це 1 десяток і 7 одиниць, 10 — це 1 десяток; від 1 десятка і 7 одиниць віднімаємо 1 десяток, залишається 7 одиниць...
Переносимо спосіб міркування (для віднімання від числа другого десятка його десятків або одиниць) на двоцифрові числа першої сотні.
Пропонуємо учням практичну роботу, під час якої учні від числа другого десятка віднімають або його одиниці, або його десятки, ілюструючи виконувані дії кружками-намистинками:
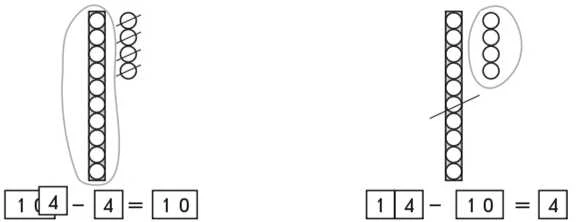
Коментар. Було 14. Число 14 складається з 1 десятка та 4 одиниць. З 1 десятка і 4 одиниць вилучили — відняли його одиниці, залишився 1 десяток.
Число 14 — це 1 десяток і 4 одиниці. З 1 десятка і 4 одиниць вилучили 1 десяток, залишилося 4 одиниці.
Ілюструємо кружками-намистинками число 54. З’ясовуємо, що змінилося число десятків. Обговорюємо, чи можна при відніманні від числа 54 його десятків або його одиниць міркувати так само, як і у випадку з числом 14.
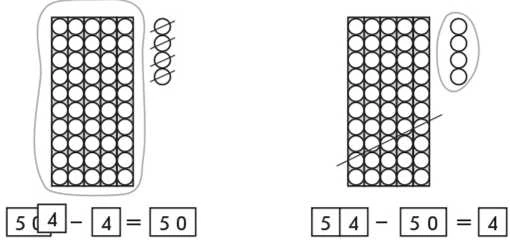
Коментар. 54 — це 5 десятків і 4 одиниці. З 5 десятків і 4 одиниць вилучили 4 одиниці, залишається 5 десятків — 50. Рівність складено правильно, вилучити — означає відняти.
54 — це 5 десятків і 4 одиниці. З 5 десятків і 4 одиниць вилучили 5 десятків і одержали 6 одиниць. Рівність складено правильно.

З учнями можна узагальнити способи міркування при додаванні та відніманні на підставі розрядного складу числа і скласти пам’ятку.

Це матеріал з посібника "Методика навчання математики у 1-2 класах" Скворцова, Онопрієнко
Наступна сторінка: 2.2.2. Методика вивчення додавання і від�...