Попередня сторінка: 3.1.2. Прості математичні задачі (1 клас)
Наступна сторінка: 3.2.1. Формування поняття про складену з�...
Очікувані результати навчання здобувачів освіти див. на сайті interactive.ranok.com.ua.
У 2 класі учні розв’язують прості задачі семи уже відомих видів: на конкретний зміст суми; на конкретний зміст різниці; на збільшення або зменшення числа на кілька одиниць; на різницеве порівняння; на знаходження невідомого доданка; на знаходження невідомого зменшуваного; на знаходження від’ємника.

Учні також знайомляться з простими задачами нових видів: на знаходження третього числа за сумою двох даних чисел; на знаходження суми трьох доданків; на конкретний зміст добутку; на конкретний зміст дії ділення (ділення на рівні частини; ділення на вміщення).
Робота над простими задачами в 2 класі відбувається за па-мяткою № 2 «Працюю над задачею».
ПАМ’ЯТКА № 2 Працюю над задачею
1. Прочитай задачу. Про що йдеться в задачі?
2. Виділи ключові слова та склади короткий запис задачі.
3. За коротким записом поясни числові дані задачі та шукане. Виконай схему.
4. Повтори запитання задачі. Що достатньо знати, щоб на нього відповісти?
Достатньо знати два числових значення:

5. Якою арифметичною дією відповімо на запитання задачі?
6. Запиши розв’язання задачі.
7. Запиши відповідь.
Розглянемо методику введення нових видів задач докладно.
ВИДИ ПРОСТИХ ЗАДАЧ У 2 КЛАСІ
1. Задачі на знаходження суми трьох доданків
У процесі підготовчої роботи до ознайомлення з цим видом задач розв’язуються задачі на конкретний зміст суми із запитанням «Скільки всього?». Наприклад, учні ознайомлюються з такими задачами.
1. Розв'яжіть задачі.
1) Юрко вирізав для аплікацій 5 трикутників і 6 чотирикутників. Скільки всього фігур вирізав Юрко?
2) Юрко вирізав для аплікацій 5 трикутників, 3 круги і 6 чотирикутників. Скільки всього фігур вирізав Юрко?
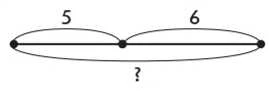
Порівнюючи задачу 2 із задачею 1, учні з’ясовують, що в задачі 1 Юрко вирізав два види фігур, а в задачі 2 — три види. Тож у короткому записі задачі 1 буде два ключових слова, а в задачі 2 — три ключових слова. Обидві задачі містять однакові запитання: «Скільки всього фігур вирізав Юрко?». Таке запитання позначається на короткому записі фігурною дужкою. Учні вносять зміни в короткий запис задачі 1 і, пояснюючи числа задачі й шукане, вносять зміни у схему.
Після складання короткого запису задачі 2 можна запропонувати учням розглянути опорну схему та схему таких задач.
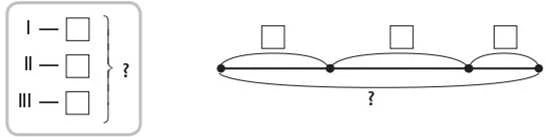
Наступним кроком визначається вплив зміни умови задачі на її розв’язання: діти визначають, що для відповіді на запитання задачі 2 достатньо знати три числових значення: І — скільки трикутників вирізав Юрко (відомо, 5); II — скільки кругів (відомо, 3); III — скільки чотирикутників (відомо, 6). Дією додавання відповімо на запитання задачі. Отже, схема аналізу має такий вигляд.
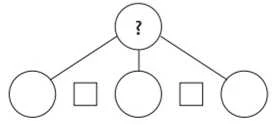
Учні вносять зміни в розв’язання задачі 1 так, щоб отримати розв’язання задачі 2; формулюють відповідь на запитання задачі 2. Порівнюючи задачі 1 і 2, школярі визначають спільне: обидві задачі на знаходження суми, але в задачі 1 потрібно було знайти суму двох доданків, а в задачі 2 — суму трьох доданків. Можна повідомити учням, що це задача на знаходження суми трьох доданків.
Щоб закріпити матеріал, пропонуємо учням працювати над задачами за пам’яткою № 2 «Працюю над задачею». Такі задачі доцільно порівнювати із задачами на знаходження суми двох доданків, що містять зайве числове дане.
Розв'яжіть задачу.
У бабусі 9 курей, 7 гусей і 5 кролів. Скільки всього птахів у бабусі?
До цієї задачі можна: 1) змінити умову задачі так, щоб числових даних було достатньо для відповіді на запитання задачі; 2) змінити запитання задачі так, щоб усі числові дані брали участь у розв’язанні.
З метою підготовки до введення задач на конкретний зміст добутку серед задач на знаходження суми трьох доданків можна пропонувати дітям задачі на знаходження суми однакових доданків з обов’язковим аналізом виразу до задачі.
2. Задачі на знаходження третього числа за сумою двох даних чисел
На етапі підготовчої роботи до ознайомлення з цим видом простих задач учням пропонуються, наприклад, такі завдання.
1. На столі лежать 2 трикутники і 3 круги. Намалюйте в зошиті стільки квадратів, скільки трикутників і кругів разом.
Учні повинні усвідомити, що для того щоб дізнатися, скільки потрібно намалювати квадратів, треба міркувати так: квадратів стільки, скільки трикутників і кругів разом; трикутників і кругів разом 2 і ще 3 (тобто 5), тому квадратів теж 5. Або: учні можуть діяти практично, тоді слід викласти на парті трикутники і круги в рядок, а під ними квадрати — так, щоб кожному трикутнику і кожному кругу відповідав тільки один квадрат (тобто учні складають пари). Але після такої роботи слід промовити міркування, а практичні дії супроводити схемою.
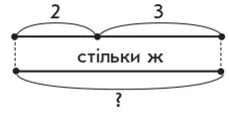
На етапі ознайомлення можна запропонувати таку задачу.
2. Розв'яжіть задачу.
Біля ставка росло 9 верб, 2 осики, а вільх стільки, скільки верб і осик разом. Скільки вільх росло біля ставка?
Прочитайте задачу. Про що йдеться в задачі? [Про верби, осики і вільхи. Росло 9 верб, 2 осики, а вільх стільки, скільки верб і осик разом. Запитується, скільки росло вільх.]
Виділіть ключові слова та складіть короткий запис задачі. [Ключові слова: «верби», «осики», «вільхи».] Запишемо ключові слова у стовпчик. Чи відомо з умови, скільки росло верб? [Відомо — 9.] Запишемо це поряд зі словом «Верби». Чи відомо, скільки росло осик? [Відомо — 2.] Запишемо це поряд зі словом «Осики». Чи відомо, скільки було вільх? [Ні, не відомо.] Що відомо з умови про вільхи? [Вільх було стільки, скільки верб і осик разом.] Як це позначимо в короткому записі? Якщо говориться «разом», то ми це позначаємо фігурною дужкою, тобто те, що стосується верб і осик, ми маємо об’єднати фігурною дужкою і посередині записати, що це число дорівнює числу вільх. Отже, короткий запис має такий вигляд:
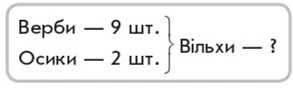
За коротким записом поясніть числові дані задачі та запитання. Що означає число 9? [Число 9 означає, скільки росло верб.] Що означає число 2? [Число 2 означає, скільки росло осик.] Розгляньте опорну схему до цієї задачі.

Що позначає фігурна дужка? [Фігурна дужка позначає, що вільх стільки, скільки верб і осик разом.] Яке запитання задачі? [Скільки росло вільх?]
Виконаємо схему. Скільки верб росло біля ставка? Як показати, що біля ставка росло 9 верб? Скільки росло осик? Як це показати: потрібно об’єднувати чи вилучати? Скільки вільх росло біля ставка? [Стільки ж, скільки верб і осик разом.] Як це показати на схемі? [Треба нижче накреслити відрізок такої самої довжини, що й відрізок, який показує, скільки верб і осик разом.] Повторіть запитання задачі. Що потрібно знати, щоб на нього відповісти? [Треба знати:
І — скільки було верб і осик разом (поки не відомо), II — що вільх було стільки ж.]
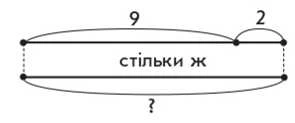
Тут дія не виконується, натомість здійснюється логічний перехід до запитання: «Скільки верб і осик разом?». Що потрібно знати, щоб відповісти на це запитання? [Потрібно знати два числових значення: І — скільки верб (9), II — скільки осик (2).] За допомогою якої арифметичної дії відповімо на запитання? [Відповімо дією додавання.]

Запишіть розв’язання задачі. [Розв’язання: 9 + 2 = 11 (шт.) — стільки ж вільх.]
Запишіть відповідь. [Відповідь: 11 вільх росло.]
Для формування умінь і навичок розв’язувати задачі цього виду учні працюють над задачами за пам’яткою № 2 «Працюю над задачею». Корисно порівняти задачі на знаходження третього числа за сумою двох даних чисел і задачі на знаходження суми трьох доданків. Наприклад:
3. Розв'яжіть задачі.
1) На клумбі розцвіли айстри. Білих айстр 7 штук, рожевих — 5 штук, а бузкових — стільки, скільки білих і рожевих айстр разом. Скільки бузкових айстр розцвіло на клумбі?
2) На клумбі розцвіли айстри. Білих айстр 7 штук, рожевих — 5 штук, а бузкових — 12. Скільки всього айстр розцвіло на клумбі?
Задачі на знаходження третього числа за сумою двох чисел
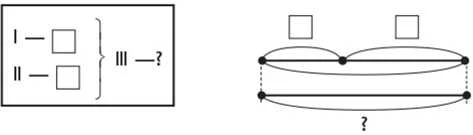
Задачі на знаходження суми трьох доданків
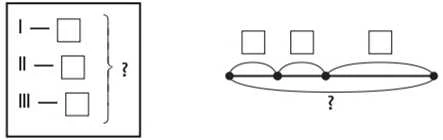
Методику ознайомлення молодших школярів із задачами на конкретний зміст добутку та частки (ділення на рівні частини та ділення на вміщення) вже докладно розглянуто в темі «Табличне множення та ділення».
МЕТОДИКА ВВЕДЕННЯ ПОНЯТТЯ ПРО ОБЕРНЕНУ ЗАДАЧУ
На прикладі порівняння задачі на знаходження суми та задачі на знаходження невідомого доданка вводиться поняття «обернена задача». Це можна зробити за допомогою таких задач:
Розв'яжіть задачі.
1) Каструля містить 5 л води, а бідон — 3 л. Скільки літрів води містять разом каструля й бідон? [5 + 3=8 (л).]
2) Каструля й бідон разом містять 8 л води. Каструля містить 5 л води. Скільки літрів води містить бідон? [8-5 = 3 (л).]
Аналізуємо з учнями, чим схожі ці задачі і чим вони відрізняються. Як склали задачу 2 із задачі 1? Задача 2 обернена до задачі 1. Складаємо ще одну задачу, обернену до задачі 1. Відповідаючи на запитання: «Що спільне та відмінне в цих задачах?», учні мають зазначити, що спільним є те, що в обох задачах ідеться про одну й ту саму ситуацію. Є каструля й бідон, у них налито воду; відмінним є те, що в задачі 1 відомо, скільки літрів води
вміщує каструля та скільки бідон; запитується, скільки всього літрів води вміщують каструля і бідон. У задачі 2 також відомо, скільки літрів води вміщує каструля, але невідомо, скільки літрів води вміщує бідон, зате указано, скільки літрів води в каструлі та бідоні разом.
Тут корисно виписати числа задачі й пояснити, що означає кожне число: 5, 3, 8. Потім невідоме число і задачі 1, і задачі 2 закрити знаком питання і сформулювати задачі. Далі слід запитати: «Яке ще число можна закрити знаком питання?», запропонувати скласти задачу, у якій запитується про це значення. Таким чином, ми розкриваємо учням технологію складання взаємно обернених задач.
|
ПАМ’ЯТКА |
|
|
Складаю взаємно обернені задачі |
|
|
1) |
виписую числа задачі і пояснюю кожне число; |
|
2) |
замінюю одне із даних чисел знаком питання; |
|
3) |
складаю задачу, у якій запитується про це значення |
Після цього можна обговорити питання про те, чим цікаві ці три задачі. [У них ідеться про одну й ту саму ситуацію, у них подано однакові числа, але те, що було відомим у задачі 1, стало невідомим у задачі 2, і навпаки.] Відповідаючи на запитання: «Як утворили задачу 2 із задачі 1?», учні повинні сказати, що те, що було невідомим у задачі 1 (кількість літрів води в каструлі й бідоні разом), стало відомим у задачі 2, а те, що було відомим у задачі 1 (кількість літрів води в бідоні), стало невідомим у задачі 2. Учитель повідомляє, що такі задачі називаються оберненими.
Отже, щоб скласти обернену задачу, слід виписати числа задачі, пояснити їх і припустити, що одне з поданих в умові задачі чисел є невідомим; скласти задачу, у якій запитується про це число. Обернених задач може бути стільки, скільки числових даних є в задачі.
Учні складають ще одну обернену задачу:
Каструля і бідон разом містять 8 л води. Бідон містить 3 л води.
Скільки літрів води містить каструля? [8 — 3= 5 (л).]
Отже, тепер до кожної простої задачі вони мають самостійно складати по дві обернені задачі. Розв’язок обернених задач розглядається як перевірка правильного розв’язання даної задачі.
Це матеріал з посібника "Методика навчання математики у 1-2 класах" Скворцова, Онопрієнко
Наступна сторінка: 3.2.1. Формування поняття про складену з�...