Прискорення. У нерівномірному русі швидкість (пам’ятайте, що ми маємо на увазі миттєву швидкість, але слово «миттєва» для спрощення не вживатимемо) у різних точках траєкторії і в різні моменти часу — різна. Тобто швидкість постійно змінюється від точки до точки, від одного моменту часу до наступного.

Під час руху швидкість може змінюватись і дуже стрімко, і порівняно повільно. Очевидно, що для характеристики стрімкості зміни швидкості має існувати певна фізична величина. У фізиці цю величину називають

прискоренням.

Прискорення а — векторна фізична величина, що характеризує стрімкість зміни швидкості руху точки (і за числовим значенням, і за напрямком) і визначається відношенням зміни швидкості тіла до інтервалу часу, протягом якого відбулася ця зміна:

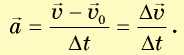
Тут v₀ — початкова швидкість руху тіла, v — його кінцева швидкість, Δt — інтервал часу, протягом якого відбулася зміна швидкості.

Одиниця прискорення — метр за секунду в квадраті:

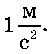
Оскільки прискорення характеризує стрімкість зміни швидкості тіла під час його нерівномірного руху, а сама швидкість характеризує стрімкість зміни положення (координати) тіла, то ці величини певним чином пов’язані одна з одною.

Величина

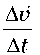
дорівнює середній за час Δt стрімкості зміни швидкості

руху матеріальної точки. Її називають середнім прискоренням.

Якщо зменшувати інтервал часу, за який змінюється швидкість, то що меншим буде цей інтервал Δt ^ 0, то меншою буде зміна швидкості

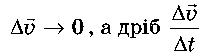
прямує до деякого граничного значення. Цю границю

називають миттєвим прискоренням точки в певний момент часу:

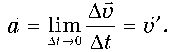
Рівноприскорений прямолінійний рух. Пригадаймо означення рівно-прискореного руху.

Рух тіла, під час якого за будь-які однакові інтервали часу швидкість руху тіла змінюється однаково, тобто прискорення під час руху тіла залишається весь час сталим за напрямком і числовим значенням (а = const), називається рівноприскореним.

Швидкість і переміщення рівноприскореного руху. З формул для прискорення легко отримати кінематичне рівняння швидкості для рівноприскореного руху:

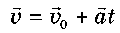
або в проекціях на вибрану вісь Х:

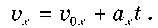
Пригадаємо формули для визначення переміщення, відомі вам з 9 класу. У кожній з формул проекції:

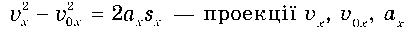
можуть бути як додатними, так і від’ємними — залежно від того, як напрямлені вектори v, v₀, а відносно осі Х.

Для прямолінійного руху проекція вектора переміщення визначається за формулою s_x = x - x₀, тоді кінематичне рівняння координати для рівноприскореного руху таке:

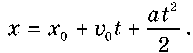
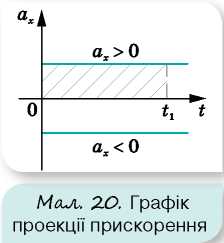
Графік проекції прискорення a_x = a_x(t). Оскільки під час рівноприскореного руху прискорення є величиною сталою, то графіком залежності проекції прискорення від часу є пряма, паралельна осі часу (мал. 20).

Якщо v₀ = 0, то за площею фігури, обмеженої графіком і перпендикуляром, опущеним на вісь часу, можна визначити швидкість руху тіла в даний момент часу t₁.

Графік проекції швидкості v_x = v_x(t). Як видно з рівняння v_x = v_0x + at, залежність проекції швидкості від часу лінійна, тому графіком є пряма (мал. 21). (Порівняйте з відомим вам графіком функції y = ax + b.)

Кут нахилу графіка до осі часу визначається числовим значенням прискорення, яке графічно

може бути визначено так:

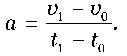
За площею фігури, обмеженої графіком швидкості та перпендикуляром, опущеним на вісь часу, можна визначити довжину пройденого шляху на даний момент часу t₁. Також, маючи даний графік, можна записати закон руху.

Залежно від проекції прискорення та початкової швидкості руху тіла графік v_x(t) матиме різний вигляд.

Графіки проекції переміщення s_x = s_x(t) і координати x = x(t) Кінематичні рівняння проекції переміщення

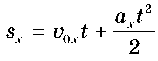
і координати

є квадратними рівняннями вигляду y = c + bx + ax², тому

графіками залежності проекції переміщення й координати від часу є параболи. Розміщення цих парабол залежно від параметрів руху є різним.

МАТЕМАТИЧНА ДОВІДКА

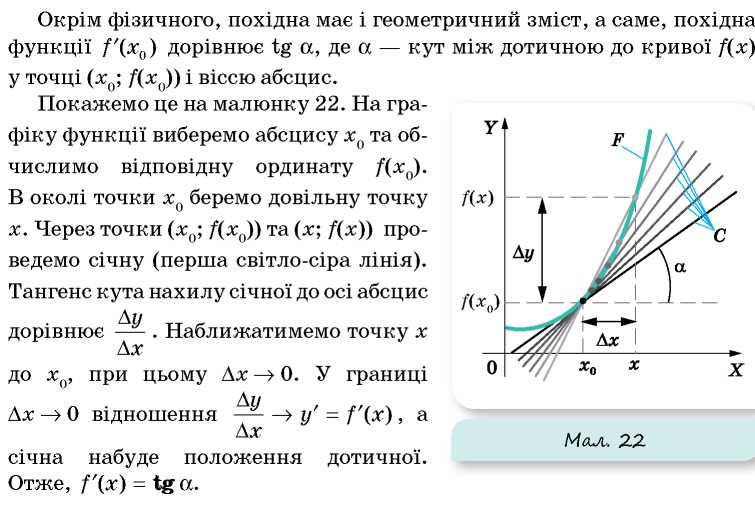
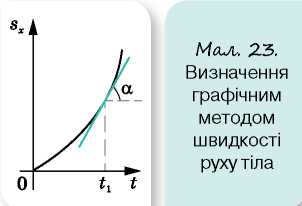
Застосуємо цю властивість похідної до залежності переміщення від часу s_x = s_x(t). Швидкість руху тіла в даний момент часу t₁ визначається тангенсом кута між дотичною до графіка проекції переміщення та віссю часу (мал. 23).

Отже, за зміною кута нахилу дотичних до графіка s_x(t) можна прослідкувати за зміною швидкості руху тіла.

ЗНАЮ, вмію, розумію

1. За будь-якого нерівномірного руху змінюється швидкість. Як прискорення характеризує цю зміну?

2. Як спрямовано вектор прискорення при прямолінійному рівнозмінному русі? У якому випадку проекція прискорення має додатне, а в якому — від’ємне значення?

3. Швидкість прямолінійного руху тіла щосекунди збільшується на 2 %: а) від початкового значення; б) від значення швидкості на початку кожної секунди. Чи стале прискорення тіла в обох випадках?

4. Тіло починає рухатися зі стану спокою прямолінійно, проходячи щосекунди шлях, на 1 м більший, ніж за попередню секунду. Чи стале прискорення тіла?

5. Чи можуть два тіла, які рухаються по одній прямій у протилежних напрямках, мати однакові вектори прискорень?

6. У яких випадках графік проекції швидкості рівноприскореного руху здіймається вгору, а в яких — спадає? Який фізичний зміст має перетин графіком проекції швидкості осі часу?

7. Яку форму має графік проекції переміщення? Чим відрізняються графіки проекції переміщення й координати?

8. Розкажіть, як за графіками прискорення, швидкості та переміщення визначити:

а) швидкість у будь-який момент часу за графіком прискорення;

б) закон руху за графіком швидкості;

в) зміну швидкості за графіком переміщення;

г) прискорення за графіком швидкості.

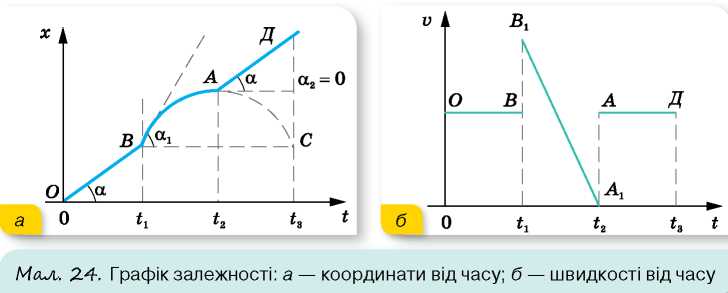
Приклади розв'язування задач Задача. За графіком руху тіла ОВАД (мал. 24, а, ділянка ВА — парабола), накресліть графік залежності швидкості руху тіла від часу та схарактеризуйте його.

Розв’язання:

Проаналізуємо графік залежності координати від часу. Протягом інтервалу часу t₁ тіло рухалося рівномірно і прямолінійно (tg α = v). Від t₁ до t₂ — рівносповільнено, причому, оскільки в точках В і А спостерігаються злами, це означає, що швидкість руху тіла різко змінилася, а саме: у точці

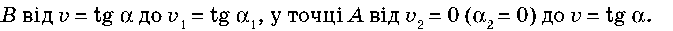
Протягом часу від t₂ до t₃ тіло рухалося рівномірно з тією самою швидкістю, що була й на початку руху.

Оскільки графік залежності координати від часу має злами, графік залежності швидкості руху від часу матиме розриви в моменти часу t₁ та t₂ (мал. 24, б; с. 27).

Звичайно ж це опис ідеалізованого руху. У реальності моментам часу t₃ та t₂ мають відповідати короткі інтервали часу, коли тіло стрімко набирало швидкості.

ВПРАВА 4

1. По схилу завдовжки 100 м лижник з’їхав за 20 с, рухаючись із прискоренням

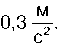
Яку швидкість мав лижник на початку і в кінці схилу?

2. Кулька, що котиться похилим жолобом зі стану спокою, за першу секунду пройшла 10 см. Який шлях кулька пройде за три секунди?

3. Визначте, у скільки разів швидкість кулі посередині ствола рушниці менша, ніж швидкість її при вильоті зі ствола.

4. Тіло, рухаючись рівноприскорено, протягом четвертої секунди пройшло 35 м. З яким прискоренням рухалось тіло? Яка його швидкість наприкінці четвертої, а також десятої секунди руху? Який шлях пройшло тіло за другу, а також за п’яту секунди? Який шлях пройшло тіло за другу і третю секунди, разом узяті?

5. Рух матеріальної точки задано рівняннями: x = 8t² + 4; y = 6t² - 3; z = 0. Визначте модулі швидкості та прискорення в момент часу t = 10 c. Скористайтесь поняттям похідної.

6. За час t = 10 c тіло пройшло шлях l = 18 м, при цьому його швидкість збільшилась у n = 5 разів. Вважаючи рух рівноприскореним, визначте прискорення тіла.

7. Тіло починає рух з точки А й рухається спершу рівноприскорено протягом часу t₀, а потім з тим самим за модулем прискоренням — рівносповільнено. Через який час від початку руху тіло повернеться в точку А?

8. Доведіть, що під час прямолінійного рівноприскореного руху без початкової швидкості справджується рівність: s₁ : s₂ : ... : s_n = 1 : 3 : ... : (2n - 1) — відстані, які проходить тіло за послідовні однакові інтервали часу, відносяться як послідовні непарні числа.

9. Рухи матеріальних точок задано такими рівняннями: а) x₁ = 10t + 0,4t²; б) x₂ = 2t - t²; в) x₃ = -4t + 2t²; г) x₄ = -t - 6t² (усі величини задано в СІ). Напишіть залежність v = v(t) для кожного випадку, побудуйте графіки цих залежностей, визначте вид руху в кожному випадку.

10. Дитина з'їхала на санчатах із гори, що має схил 40 м, за 10 с, а потім проїхала по горизонтальній ділянці ще 20 м і зупинилася. Обчисліть швидкість у кінці схилу, прискорення на кожній ділянці, загальний час руху та середню швидкість на всьому шляху. Накресліть графік швидкості.

11. Велосипедист перші 4 с рухався зі стану спокою з прискоренням

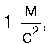
а потім

0,1 хв їхав рівномірно, а останні 20 м до зупинки — рівносповільнено. Обчисліть середню швидкість за весь час руху. Побудуйте графік v_x(t).

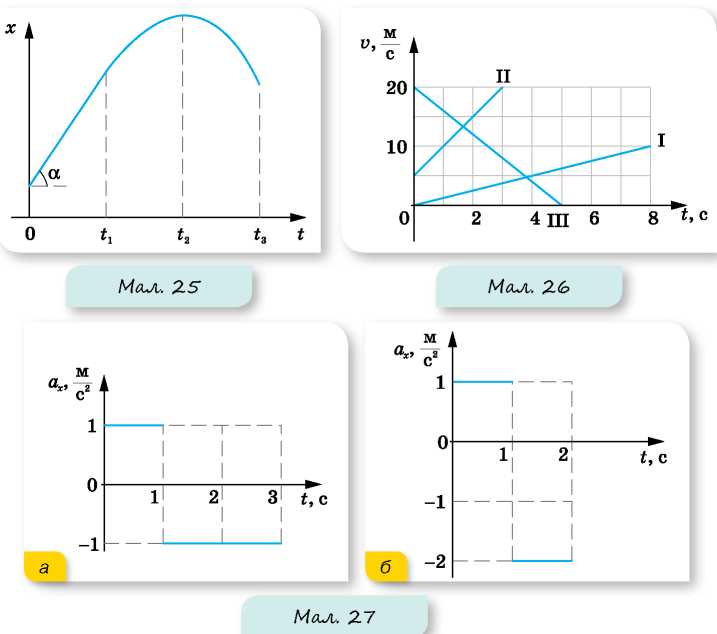
12. На малюнку 25 наведено графік залежності координати тіла від часу. Після моменту часу t крива графіка — парабола. Який рух зображено на цьому графіку? Побудуйте графік залежності швидкості тіла від часу.

13. За наведеними на малюнку 26 графіками напишіть рівняння залежностей v_x = v_x(t) і х = x(t). Вважайте, що в початковий момент (t = 0) тіло перебуває в початку координат (х = 0). Побудуйте графіки залежності х = x(t) для кожного з тіл.

14. За графіками залежності a_x(t), наведеними на малюнку 27, а і б побудуйте графіки v_x(t), вважаючи, що в початковий момент часу (t = 0) швидкість руху матеріальної точки дорівнює нулю.

15. Рухи двох автомобілів по шосе описуються рівняннями х₁ = 2t + 0,2t² і х₂ = 80 - 4t. Опишіть картину руху; визначте час і місце зустрічі автомобілів; відстань між ними через 5 с; координату першого автомобіля в той момент часу, коли другий перебував у точці початку відліку. Розв’яжіть задачу аналітично та графічно.

16. Матеріальна точка рухається вздовж осі Х зі швидкістю v (мал. 28, с. 30). Один під одним накресліть графіки проекцій прискорення a_x(t), переміщення s_x(t) та пройденого шляху l(t). Визначте середнє значення модуля швидкості за час руху від t = 0 до t = 2τ.

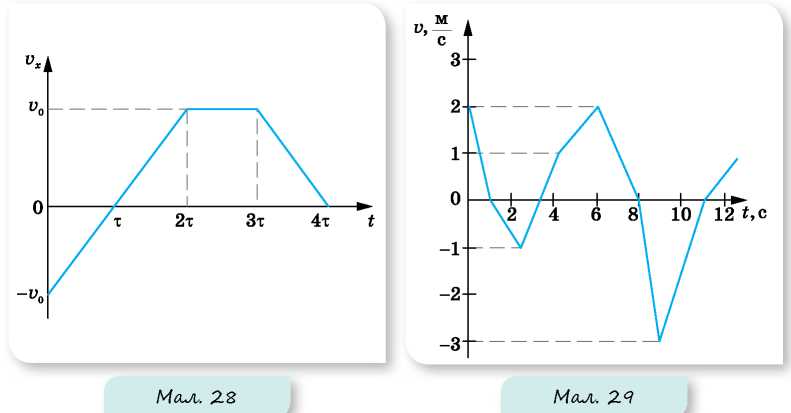
17. На малюнку 29 (с. 30) наведено графік швидкості тіла, яке рухається прямолінійно. На яку максимальну відстань від початкового положення перемістилось тіло за час руху?

18. Накресліть графік залежності координати від часу для прямолінійного руху, що одночасно задовольняє дві вимоги: а) протягом інтервалу часу від 2 до 6 с середня

швидкість руху дорівнює

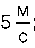
б) максимальна швидкість протягом цього ж інтерва

лу часу дорівнює

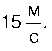
Експериментуємо

Кулька скочується по жолобу з уклоном 0,3 (уклон — це відношення висоти жолоба до його довжини). Визначте: максимальну швидкість руху кульки; швидкість у середній точці жолоба; прискорення кульки. Дослідіть залежність прискорення руху кульки від кута нахилу жолоба.

 

 

Це матеріал з підручника Фізика і астрономія за 10 клас Засєкіна (профільний рівень)